Pen-and-paper Nomic

The pen-and-paper game of Nomic (by Peter Suber) has an initial ruleset which describes how one proposes changes to the rules, how one gets those changes ratified, a way to award points when someone’s rule change is ratified, and a rule declaring that the winner is the first player to amass 100 points. Some of the rules are mutable and some are immutable and there are rules about turning mutable rules into immutable ones and vice-versa.

The game was meant to show some of the paradoxes of self-amendment. It was meant to lead people into situations where it was clear that certain actions were both legal (or even mandatory) and illegal.

A drastically simplified starting set of rules might look like:

• There are these players: Alice, Bob, Carol, David, and Mel.
• Any of the players can propose a change to these rules at any time when there is not already an outstanding proposal.
• When a player makes a proposal, all players (including the player making the proposal) must immediately vote: Yay or Nay.
• If a proposal garners more Yay than Nay votes, it takes effect immediately. Otherwise, the proposal is rejected.
• The winner is the first person to score 100 points.

Nomic in Code

So, 30 years ago, I had the idea that it would be fabulous to write some code to referee a Nomic game. However, because interpretation of the rules is so horrendously human, it felt impossible. Today, in 2026, it seems one could maybe get Claude, Gemini, or some other LLM to referee. But, this doesn’t much interest me, either, really. I cannot get any of them to keep track of something that I made them write down. I cannot imagine that I would be happy with their interpretation of whether my move is legal given the current state of the rules nor to amend the rules appropriately if my move is legal.

What felt slightly more attainable 30 years ago would be to make it a battle in code:

• The players propose deltas to the current code.
• The players vote on which deltas to approve.
• If the resulting code declares you the winner, you win.

This was nice and all, but it was also too static. The rules about who can vote and how votes are tallied and such wouldn’t be subject to change.

Nomic in Code in 2026

Fast-forward to last month. Last month, I realized that with the GitHub API interface, I could implement a very Nomic-ish pull request battle game. I can:

• Gather information about all of the open pull requests on a repository,
• Checkout a copy of the current main branch of that same repository,
• Run the code on the main branch of that repository and give it the information that I collected about the open pull requests, and
• Have the code on the main branch tell me which open pull requests (if any) to accept or reject.

To be truly in Nomic’s full spirit, it would be nice to allow the code in the repository to interact with the GitHub API on its own. Alas, that would immediately let the players vote in changes that expose my GitHub tokens, so it would be a gaping security hole—not only because it would let users impersonate me but because it would let them end-around the actual code in the repository to make changes to the main branch in the repository.

So, as it is, I have a supervisor written in Common Lisp which handles all of the interaction with GitHub and various game repositories (one to play in Common Lisp, one to play in JavaScript, and one to play in Python). The supervisor:

• fetches all of the open pull requests;
• annotates each pull request with:
  • all of the reviews on the pull request,
  • all of the comments on the pull request, and
  • all of the commits on the pull request;
• clones the main branch of the game repository;
• runs the game code from that main branch giving it the annotated list of open pull requests encoded as JSON on standard input;
• reads the JSON-encoded output from the game code; and
• acts accordingly.

The game code, given a list of open pull requests can reply with one of the following messages:

The "defer" decision means that there is not enough information at the moment. Maybe, in the future, with other pull requests or other comments or reviews we will be able to make some move.

If the game code replies with anything that isn’t one of the four types of replies shown above, the supervisor assumes the latest merge broke the code and reverts the change.

The Ask

I haven’t been able to drum up enough players for a game in any of my regular haunts. So, I am looking for tolerant players who will help me give it a test run or two to work out the kinks in the supervisor. Some areas where I forsee potential issues:

• There may be scenarios that cause the game to reach an impasse.
• There are probably some GitHub responses that the supervisor doesn’t do the right thing with (in fact, I think I just thought of a situation that a malicious player could do if they are a collaborator rather than doing this through forked repos).
• There might be special issues related to pull requests coming in from forks rather than within the repo which I cannot test without making myself a second GitHub account.
• Who can say what the optimal number of players is, at this point?

So, if you’re tolerant of some bumps in the process, have a GitHub account (or will make one), and are interested in a Common Lisp battle of pull requests, let me know so we can get a game going.

The post Nomic Coding Game first appeared on nklein software.

There are still a few of us (at least two) who are using MK:DEFSYSTEM. The venerable system construction tool has accumulated a lot of ancient cruft, some of which quite convoluted.

Recently I went back to MK:DEFSYSTEM and "cleaned up" some of the code, especially regarding the pathname construction for each component.  I also used some simpler hierarchical tricks using defstruct only.

The result should be more solid and clearer in the steps that comprise some "macro tasks". Of course, a rewrite using CLOS would change the coding style, but the choice has been made to keep the MK:DEFSYSTEM code base quite... retro (and somewhat simple).

Why did I went back to MK:DEFSYSTEM? As usual, it is because of a rabbit-hole I fell into: I will blog about it later on (hint: HEΛP).

MK-DEFSYSTEM quick history as of March 2026

MK-DEFSYSTEM (or MK:DEFSYSTEM, or MAKE:DEFSYSTEM) was originally written by Mark Kantrowitz as part of the original "CMU Lisp Utilities" collection; an early "public" set of Common Lisp code and utilities that, in the writer's opinion form one of the basis of most Common Lisp writing to date.

As stated (by M. Kantrowitz himself) in this file header, the original version of MK-DEFSYSTEM was inspired by the Symbolics DEFSYSTEM (or DEFSYS) tool. Yet, MK-DEFSYSTEM differs significantly from it.

In its original form, MK-DEFSYSTEM was built in the CLtL1 era, accommodated a lot of variance among filesystems and CL implementations and it still bears those idiosycrasies. CLtL2 (1992) first and ANSI (1994) next, started reshaping the code base then.

MK-DEFSYSTEM was originally distributed under a license agreement that made redistribution tricky. In 1999, the writer - that'd be me, Marco Antoniotti - contacted Mark Kantrowitz offering to become a maintainer while reworking the distribution license to hammer some FOSS into it. Mark Kantrowitz graciously agreed and, after that, the writer got literally and physically hugged by a few Common Lisp developers because they could use MK-DEFSYSTEM more freely.

Of course, ASDF came along and it solved the same problems that Symbolics (and Kent Pitman's) DEFSYS and MK-DEFSYSTEM solve, plus much more.

Yet, MK-DEFSYSTEM has some nice features (in the eye of the beholder).

MK-DEFSYSTEM still ships in one file - defsystem.lisp - that you can LOAD in your Common Lisp init file. Of course, a big chunk of its current code base is "backward compatibility" and new ok-we-miss-UIOP-and-or-at-least-CL-FAD functionality, plus an ever growing ongoing commentary like this one.

Given this background, the writer has been maintaining MK-DEFSYSTEM for a long time, and more recently, Madhu has made significant changes (and maintains himself a fork with some bells and whistles of his own) since 2008.

Of course, many other contributors helped over the years, and are acknowledged in the early Change Log and in comments in the code.

In early 2026, the writer cleaned up the code and reworked some of the logic, by factoring out some code from main functions. In particular, the CREATE-COMPONENT-PATHNAMES, GENERATE-COMPONENT-PATHNAMES, COMPONENT-FULL-PATHNAME, COMPONENT-FULL-NAMESTRING interplay is better organized; plus new structures, leveraging DEFSTRUCT :INCLUDE feature have been introduced, rendering the code TYPECASE-able.

MK-DEFSYSTEM is old, but it works. It is quirky but it works (at least for the two or three known users - which, in 2026, is already a big chunk of the Common Lisp users' community). Moreover, it does have, at least in the eye of the beholder, some more user friendly user API, for most use case, especially for plain Common Lisp code.

The current MK-DEFSYSTEM repository is at https://gitlab.common-lisp.net/mantoniotti/mk-defsystem

(*) It is assumed that the reader knows about all the acronyms, tools and systems referred to in the text.

'(cheers)

When talking to Lisp programmers, you often hear something like, “adapt Lisp to your problem, not your problem to Lisp.” The basic idea is this: if Lisp doesn’t let you easily write a solution to your problem because it lacks some fundamental constructs that make expressing solutions easy, then add them to Lisp first, then write your solution.

That sounds all good and well in the abstract, and maybe we could even come up with some toy examples—say, defining HTTP request routing logic in a nice DSL. But where’s a real example of this that’s not artificial or overengineered?

Recently, on Twitter, I butted into the middle of an exchange between @Ngnghm (a famous Lisp programmer) and @korulang (an account dedicated to a new language called Koru) about Lisp. I’m oversimplifying, but it went something like this:

• Lisp is slow.
• No it’s not!
• Yes it is!
• No it’s not!
• Then prove it!

Now, there’s plenty of evidence online that Common Lisp has reasonably good compilers that produce reasonably good machine code, and so the question became more nuanced: Can Lisp be realistically competitive with C without ending up being a mess of unidiomatic code?

Our interlocutor @korulang proposed a benchmark, the “nbody” benchmark from the Computer Language Benchmarks Game. This was of particular interest to them, because they used it as an object of study for their Koru language. To quote their blog post:

We wanted Koru kernels to land in the same ballpark as idiomatic C, Rust, and Zig.

The result was stronger than that.

Our fused n-body kernel, written in straightforward Koru kernel style, came in faster than the plain reference implementations. Every implementation here is "naive" — the obvious, idiomatic version a competent programmer would write in each language. No tricks, no hand-tuning, no -ffast-math: […]

and they proceeded to show Koru being 14% faster than C and 106% faster than Lisp.

Now, putting aside that some of the code and blog post were written with LLMs, there are many questions that are left unanswered here, since computer architecture and operating system matter a lot (where did these benchmarks run?). Moreover, the author buries the lede a little bit and proceeds to show how we might write “unidiomatic” C to match the performance of Koru.

I’m not concerned about nitpicking their approach or rigorously evaluating their claims, but I would like to dwell on this common refrain: “idiomatic”. What is that supposed to mean?

“Idiomatic code” in the context of programming means something like “representative of a fluent computer programmer” and “aligned with the peculiar characteristics of the language”. In some sense, idiomatic code in a particular language shouldn’t stand out amongst other code in that language, and idiomatic code should, in some sense, portray the identity of the language itself.

Idiomatic C is the C that uses terse names, simple loops, and unsafe arithmetic.

Idiomatic Haskell is the Haskell that uses short functions, higher-order abstractions, immutable data structures, and safe constructs.

What about idiomatic Lisp? Well, here’s the rub. A fluent programmer at Lisp doesn’t reach for one paradigmatic toolbox; they weave in and out of imperative, functional, object-oriented, etc. styles without much of a second thought. There’s a sort of “meta” characteristic to Lisp programming: you’re programming the language almost as much as you’re programming the program.

Yes, Lisp has loops, but “loopy code” isn’t intrinsically “Lispy code”. Yes, Lisp has objects, but “OOPy code” isn’t intrinsically “Lispy code”. In my opinion, what makes code “Lispy” is whether or not the programmer used Lisp’s metaprogramming and/or built-in multi-paradigm facilities to a reasonable degree to make the solution to their problem efficient and easy to understand in some global sense. For some problems, that may be “loopy” or “OOPy” or something else. It’s finding a Pareto-efficient syntactic and semantic combination offered by the language, or perhaps one of the programmer’s own creation.

So we get back to the @korulang benchmark challenge. Looking at their repository:

• nbody.c looks like idiomatic C;
• nbody.hs looks like wildly unidiomatic Haskell, but the problem is, the idiomatic version would probably be slower;
• nbody.lisp looks reasonable, though it could easily be improved, but loopy; and
• The Koru solution kernel_fused.kz looks idiomatic, as far as I can tell for not knowing anything about Koru.

I hesitate to say nbody.lisp is idiomatic. It’s reasonable, it’s straightforward to any imperative-minded programmer, but it’s not Lispy. That doesn’t make it good or bad, but it does lead to the grand question:

Can we use Common Lisp to express a solution to the nbody benchmark in a way that reads more naturally than a direct-from-C port?

I would say that, at face value, Koru’s solution is along the lines of what is more natural relative to the problem itself. Here are the essential bits.

~std.kernel:shape(Body) {
x: f64, y: f64, z: f64,
vx: f64, vy: f64, vz: f64,
mass: f64,
}
~std.kernel:init(Body) {
{ x: 0, y: 0, z: 0, vx: 0, vy: 0, vz: 0, mass: SOLAR_MASS },
{ x: 4.84143144246472090e+00, y: -1.16032004402742839e+00, z: -1.03622044471123109e-01, vx: 1.66007664274403694e-03 * DAYS_PER_YEAR, vy: 7.69901118419740425e-03 * DAYS_PER_YEAR, vz: -6.90460016972063023e-05 * DAYS_PER_YEAR, mass: 9.54791938424326609e-04 * SOLAR_MASS },
{ x: 8.34336671824457987e+00, y: 4.12479856412430479e+00, z: -4.03523417114321381e-01, vx: -2.76742510726862411e-03 * DAYS_PER_YEAR, vy: 4.99852801234917238e-03 * DAYS_PER_YEAR, vz: 2.30417297573763929e-05 * DAYS_PER_YEAR, mass: 2.85885980666130812e-04 * SOLAR_MASS },
{ x: 1.28943695621391310e+01, y: -1.51111514016986312e+01, z: -2.23307578892655734e-01, vx: 2.96460137564761618e-03 * DAYS_PER_YEAR, vy: 2.37847173959480950e-03 * DAYS_PER_YEAR, vz: -2.96589568540237556e-05 * DAYS_PER_YEAR, mass: 4.36624404335156298e-05 * SOLAR_MASS },
{ x: 1.53796971148509165e+01, y: -2.59193146099879641e+01, z: 1.79258772950371181e-01, vx: 2.68067772490389322e-03 * DAYS_PER_YEAR, vy: 1.62824170038242295e-03 * DAYS_PER_YEAR, vz: -9.51592254519715870e-05 * DAYS_PER_YEAR, mass: 5.15138902046611451e-05 * SOLAR_MASS },
}
| kernel k |>
std.kernel:step(0..iterations)
|> std.kernel:pairwise {
const dx = k.x - k.other.x;
const dy = k.y - k.other.y;
const dz = k.z - k.other.z;
const dsq = dx*dx + dy*dy + dz*dz;
const mag = DT / (dsq * @sqrt(dsq));
k.vx -= dx * k.other.mass * mag;
k.vy -= dy * k.other.mass * mag;
k.vz -= dz * k.other.mass * mag;
k.other.vx += dx * k.mass * mag;
k.other.vy += dy * k.mass * mag;
k.other.vz += dz * k.mass * mag;
}
|> std.kernel:self {
k.x += DT * k.vx;
k.y += DT * k.vy;
k.z += DT * k.vz;
}
| computed c |>
capture({ energy: @as(f64, 0) })
| as acc |>
for(0..5)
| each i |>
captured { energy: acc.energy + 0.5*c[i].mass*(c[i].vx*c[i].vx+c[i].vy*c[i].vy+c[i].vz*c[i].vz) }
|> for(i+1..5)
| each j |>
captured { energy: acc.energy - c[i].mass*c[j].mass / @sqrt((c[i].x-c[j].x)*(c[i].x-c[j].x)+(c[i].y-c[j].y)*(c[i].y-c[j].y)+(c[i].z-c[j].z)*(c[i].z-c[j].z)) }
| captured final |>
std.io:print.blk {
{{ final.energy:d:.9 }}
}

Can we achieve something similar in Lisp?

First, let’s make a baseline. I’m running Ubuntu Noble with a “AMD RYZEN AI MAX+ PRO 395” with a clock speed that varies between 0.6-5 GHz. I am also using SBCL 2.6.3 and gcc 13.3. Using nbody.lisp as a starting point, I modified it for a few easy wins. I’ll call this version nbody-lisp-conventional. A quick benchmark reveals that the loopy Lisp code is only about 20% slower than the C code compiled with gcc -O3 -ffast-math -march=native.

$ ./nbody-lisp-conventional 50000000
-0.169286396
timing: 2000 ms
$ ./nbody-c 50000000
-0.169286396
timing: 1662 ms

As a Lisp programmer, it’s not surprising that it’s a little slower. The number of person-years that have gone into C compilers to optimize idiomatic C code makes the development effort behind SBCL, the most popular open-source Lisp compiler, look like a rounding error.

Now that we have a baseline, our goal is to come up with a nicer Lisp program that also improves the timing.

Our approach will be simple. We will create a library.lisp that contains new language constructs of a similar ilk to Koru, and we will use them to implement the nbody benchmark in impl.lisp. Some rules:

• No compile-time precomputation or caching. I can’t just compute the answer at compile time, or cache a sub-computation that makes the full one trivial.
• No fundamental algorithm changes. I can’t use a different integrator, for example.
• Using assembly is allowed, but it must only make use of the facilities offered by the Lisp compiler (i.e., no external tools), and the implementation of nbody itself must be understandable without knowing assembly. In other words, it should be sufficiently hidden, and in principle easily substitutable with portable code.
• Library code must be in principle useful for other similar tasks. It should not be hyper-specialized to this specific problem instance, but instead be useful for this general class of problems.

The third rule is more rigorous than it looks. It means we can’t just have a solve-nbody problem which dispatches to assembly.

To accomplish the above, we define a kernel DSL. The DSL allows us to express how elements of a composite transform, maintaining just enough invariants to allow them to be handled efficiently. These kernels are then compiled into efficient code, more efficient than ordinary loopy Lisp allows for.

Our attention will be focused on a proof-of-concept library of functionality for writing particle simulators. The operators we define are:

• define-kernel-shape: Define the data to be transformed by each kernel. This would be the data to characterize the static and dynamic properties of a particle in motion, as well as the number of particles under consideration.
• define-kernel-step: Define a kernel as a sequence of existing ones.
• define-self-kernel: Define a read-write kernel that operates on each element independently, without access to other elements (i.e., a map operation).
• define-pairwise-kernel: Define a read-write kernel that operates on all pairs of elements, reduced by symmetry (i.e., (i,j) and (j,i) are considered only once).
• define-reduction-kernel: Define a read-only kernel that does reduction of a sequence into a single value (i.e., a reduce operation).

This collection of five operators forms a miniature, re-usable language. These broadly recapitulate those of Koru, and allow us to write something that looks like this:

(defconstant +solar-mass+ (* 4d0 pi pi))
(defconstant +days-per-year+ 365.24d0)
(defconstant +dt+ 0.01d0)
(define-kernel-shape body 5
x y z vx vy vz mass)
(defparameter *system*
(make-body-system
(list :x 0d0 :y 0d0 :z 0d0
:vx 0d0 :vy 0d0 :vz 0d0
:mass +solar-mass+)
...))
(define-pairwise-kernel advance-forces (s body dt)
(let* ((dx (- i.x j.x))
(dy (- i.y j.y))
(dz (- i.z j.z))
(dsq (+ (+ (* dx dx) (* dy dy)) (* dz dz)))
(mag (/ dt (* dsq (sqrt dsq)))))
(let ((dm-j (* mag j.mass))
(dm-i (* mag i.mass)))
(decf i.vx (* dx dm-j))
(decf i.vy (* dy dm-j))
(decf i.vz (* dz dm-j))
(incf j.vx (* dx dm-i))
(incf j.vy (* dy dm-i))
(incf j.vz (* dz dm-i)))))
(define-self-kernel advance-positions (s body dt)
(incf self.x (* dt self.vx))
(incf self.y (* dt self.vy))
(incf self.z (* dt self.vz)))
(define-reduction-kernel (energy e 0d0) (s body)
(:self
(+ e (* (* 0.5d0 self.mass)
(+ (+ (* self.vx self.vx) (* self.vy self.vy))
(* self.vz self.vz)))))
(:pair
(let* ((dx (- i.x j.x))
(dy (- i.y j.y))
(dz (- i.z j.z)))
(- e (/ (* i.mass j.mass)
(sqrt (+ (+ (* dx dx) (* dy dy))
(* dz dz))))))))
(define-kernel-step run-simulation (system body n :params ((dt double-float)))
(advance-forces dt)
(advance-positions dt))

Well, in fact, this isn’t an ideal approximation, it’s almost exactly how it turned out. Given this is a proof of concept, we sometimes have to write some Lisp things a little funny. For example, you’ll notice we write:

(+ (+ (* dx dx) (* dy dy)) (* dz dz))

instead of the far more readable

(+ (* dx dx) (* dy dy) (* dz dz))

Both are completely valid and both can be used. So why the former? It is a result of a limitation of a little feature I built in: auto-vectorization. The vectorizer walks the mathematical expressions and replaces them with fast SIMD variants instead. Here’s a little fragment showing this rewrite rule:

...
(case (car expr)
;; (+ a (* b c)) -> fmadd(a,b,c)
((+)
(let ((args (cdr expr)))
(cond
((and (= (length args) 2) (mul-p (second args)))
`(%%fmadd-pd ,(xf (first args))
,(xf (second (second args)))
,(xf (third (second args)))))
...

The implementation of these kernel macros in library.lisp weighs in at just under 700 lines, and includes optional x64 SIMD auto-vectorization.

Well, for the nail biting moment, how does it compare? I made a Makefile that compares the idiomatic C against the loopy Lisp against our kernel DSL Lisp. It does a median-of-3. Running this on my computer gives:

$ make bench
=== C (gcc -O3 -ffast-math) ===
-0.169286396
runs: 1657 1664 1653 ms
median: 1657 ms
=== Lisp (SBCL, conventional loops) ===
-0.169286396
runs: 1991 2009 2005 ms
median: 2005 ms
=== Lisp (SBCL, kernel syntax) ===
-0.169286396
runs: 1651 1651 1652 ms
median: 1651 ms

So, in fact, we have matched the performance of C almost exactly. Furthermore, the generated code is still not as lean as it could be. Not to put too fine a point on it, but, <100 lines of Lisp, supported by

• 700 lines of library code and about 4 hours of my time; and
• 500k lines of its host compiler sbcl

has performance parity and greater readability/reusability than <100 lines of C, supported by

• ~5,000k lines of just the C part of its host compiler gcc.

None of this is to make an argument that Lisp is “better”, or that there isn’t merit to avoiding custom DSLs in certain circumstances, or that the world doesn’t have room for more custom home-grown compilers and parsers, but I think this is the clearest possible, quasi-realistic demonstration that idiomatic Lisp can be as fast as idiomatic C without tremendous work, whilst netting additional benefits unique to Lisp.

All code is available here.

We are announcing a new stable ECL release. This release highlights:

• bytecodes closures are now faster and avoid capturing unused parts of the lexical environment
• improvements to the native compiler, including better separation between compiler frontend and backend, reduced function call overhead, more aggressive dead code elimination and many internal improvements and bug fixes
• hash table implementation improvements and bug fixes for collisions
• streams: extensions EXT:PEEK-BYTE, EXT:UNREAD-BYTE, GRAY:STREAM-PEEK-BYTE and GRAY:STREAM-UNREAD-BYTE, bugfixes and implementation refactor
• the codebase has been updated to conform to the C23 standard
• simplified procedure for cross-compiling ECL itself
• support for cross-compilation of Common Lisp code to different targets using a new :TARGET option for COMPILE-FILE
• some fixes for the emscripten target

The release also incorporates many other bug fixes and performance improvements as well as an updated manual. We'd like to thank all people who contributed to ECL with code, testing, issue reports and otherwise.

People listed here contributed code in this iteration: Daniel Kochmański, Marius Gerbershagen, Tarn W. Burton, Kirill A. Korinsky, Dmitry Solomennikov, Kevin Zheng, Mark Shroyer and Sebastien Marie.

People listed here did extensive release candidate testing on various platforms: Marius Gerbershagen, Daniel Kochmański, Dima Pasechnik, Matthias Köppe, Jeremy List, Mark Damon Hughes and Paul Ruetz.

This release is available for download in a form of a source code archive (we do not ship prebuilt binaries):

• ECL 26.3.27 tarball archive
• The ECL Manual

Finally, a note on the release schedule: ECL releases often take some time to come out, partially because we do extensive testing against supported platforms and existing libraries to find regressions. In the meantime all improvements are incrementally incorporated in the branch develop. It is considered stable and it is tested and reviewed with necessary dilligence. If release cycle is too slow for your needs, then we suggest following the branch develop for the most recent changes.

Happy Hacking,
The ECL Developers

Pointer-rich data layouts lead to suboptimal performance on modern hardware. For an excellent introduction to this, see the article The Road to Valhalla. While it is specifically about Java, many parts of the article also apply to other languages. To summarize some of the key points of the article:

• In 1990, a main memory fetch was about as expensive as an arithmetic operation. Now, it might be a hundred times slower.
• A pointer-rich data layout involving indirections between data at different locations is not ideal for today's hardware.
• A language should make flat (cache-efficient) and dense (memory-efficient) memory layouts possible without compromising abstraction or type safety.

Consider a vector of records (or tuples, structures, product types - I'll stay with "record" in this article). A pointer-rich layout has each record allocated separately in the heap, with a vector containing pointers to the records. For example, given a "Point" record of two numbers:

The flat and dense layout has the records directly in the array:

(Note that there is another flat layout, namely, using one vector per field of the record. This is better suited to instruction-level parallelism or specialized hardware (e.g., GPUs), especially when the record fields have different sizes. But it is less suited for general-purpose computing, as reading a single vector element requires one memory access per field, whereas the "vector of records" layout above requires only one access per record. Such a layout can be easily implemented in any language that has arrays of native types, whether in the language itself or in a library (e.g., OCaml's Owl library). Thus, in this article, I will only consider the "array of records" layout above.)

Functional language considerations

Things should be much easier in functional languages than in Java: we have purity, referential transparency, and everything is a value. So it should be simple enough to store these values in memory in their native representation. But there are reasons that that is often not the case in practice:

• Lazyness: a value can be a computation that produces a value only when needed.
• Layout polymorphism: unless we replicate the code for every type (as, for example, Rust does), we need to be able to store every possible value in the same kind of slot.
• Dynamically typed languages require type information at runtime.
• Functional languages often have automatic memory management, which may require runtime type information.
• Many of our languages are not purely functional, but contain impure features.
• Pure languages often lack traditional vectors or arrays, since making them perform well in immutable code is not easy.
• Historical reasons: Graph reduction was a common implementation technique for lazy languages, and graphs involve pointers.
• Implementation restrictions: not being mainstream, fewer resources are devoted to implementation and optimization.

Many implementations can not even lay out native types flat in records, so a Point record of IEEE 754 double-precision numbers may actually look like this in memory:

The (very short) List

So, given a record type, which functional languages allow a collection of values of that type to have a flat, linear memory layout? The number of programming languages that claim to be "functional" is huge, so the ones listed here are just a selection based on my preferences - mainly languages that allow that layout, and some I have some experience with and can speculate on how easy or hard it would be to add that as a library or extension.

Since the Point record can be misleading in its simplicity when it comes to the question of whether the functionality could be implemented as a library, I'll point out that there are records where the layout is a bit more interesting:

• Records containing different types with different storage sizes, for example, one 64-bit float and one 32-bit integer. On most architectures, this will require 4 bytes of padding between elements.
• Records containing native values along with something that has to be represented as a pointer, for example, a reference-type or a lazy value. In a flat layout, this means that every nth element will be a pointer, requiring special support from the memory management system, either by providing layout information or by using a conservative GC that treats everything as a potential pointer.

Pure languages:

Clean

Yes: Clean has unboxed arrays of records in the base language.

Caveat: it does not have integer types of specific sizes and only one floating-point type, making it harder to reduce memory usage by using the smallest type just large enough to support the required value range. It seems possible to implement such types in a library (the mTask system does that).

Futhark

No. Futhark does not intend to be a general-purpose language, so this is not surprising.

I mention it here because it does have arrays of records, but, since it targets GPUs and related hardware, it uses the "record of arrays" layout mentioned above.

Haskell

Yes. Not in the base language, but there is library support via Data.Vector.Unboxed. Types that implement the Unbox type class can be used in these vectors. Many basic types and tuples have an Unbox instance. However, when you care about efficiency, you probably do not want to use tuples but rather a data type with strict fields, i.e., not:

type Point = (Double, Double)

but:

data Point = Point !Double !Double

Writing an Unbox instance for such a type is not trivial. The vector-th-unbox library makes it easier, but requires Template Haskell. Unboxed vectors are implemented by marshalling the values to byte arrays, so records with pointer fields are not supported.

Impure Languages

F#

Yes, even records with pointer fields. Records have structural equality, and you can use structs or the [<Struct>] attribute to get a flat layout.

And that's all I could find. Unless I follow Wikipedia's list of functional programming languages, which contains languages such as C++, C#, Rust, or Swift, that allow the flat layout, but don't really fit my idea of a functional language. But SML, OCaml, Erlang (Elixir, Gleam), Scala? Not that I could see (but please correct me if I'm wrong).

Rolling your own

Since there is a library implementation for Haskell, maybe that's a possibility for other languages?

You should be able to implement flat layouts in any language that supports byte vectors. More interesting is how well such a library fits into the language, and whether a user of the library has to write code or annotations for user-defined record types, or whether the library can handle part or all of that automagically.

I'll only mention my beloved Lisp/Scheme here. Lisp's uniform syntax and macro system are a bonus here, but the lack of static typing makes things harder.

In Scheme, R6RS (and R7RS with the help of some SRFIs) has byte-vectors and marshalling to/from them in the standard library. But Scheme does not have type annotations, so you either need to offer a macro to define records with typed fields or to define how to marshal the fields of a regular (sealed) record. Since you can shadow standard procedures in a library, you can write code that looks like regular Scheme code, but, perhaps surprisingly, loses identity when storing/retrieving values from records:

(let ((vec (make-typed-vector 'point 1000))
      (pt (make-point x y)))
  (vector-set! vec 0 pt)
  (eq? (vector-ref vec 0) pt))
 ⇒ #f

(But then, you probably shouldn't be using eq? when doing functional programming in Scheme).

The same approach is possible in Common Lisp. In contrast to Scheme, it does have optional type annotations, and, together with a helper library for accessing the innards of floats and either the meta-object protocol to get type information or (probably better) a macro to define typed records, an implementation should be reasonably straightforward. Making it play nice with inheritance and the dynamic nature of Common Lisp (e.g., adding slots to classes or even changing an object's class at runtime) would be a much harder undertaking.

Conclusion

Of the functional languages I looked at, only F# fully supports flat and dense memory layouts. Among the pure languages, Haskell and Clean come close.

The question is how important this really is. There's a good argument to be made for turning to more specialized languages like Futhark if you mainly care about performance. On the other hand, having a uniform codebase in one language also has advantages.

Then, the performance story has changed, too. While the points Project Valhalla raises remain true in principle, processor designers are aware of this as well. They are doing their best to hide memory latency with techniques such as out-of-order execution or humongous caches. Thus, on a modern CPU, the effects of a pointer-rich layout are often only observable with large working set sizes.

Still, given the plethora of imperative language that can get you to Valhalla, support for this in the functional landscape seems lacking. In the future, I hope to see more languages or libraries that will make this possible.

FSet v2.3.0 added transients!  These make it faster to populate new collections with data, especially as the collections get large.  I shamelessly stole the idea from Clojure.

They are currently implemented only for the CHAMP types ch-set, ch-map, ch-2-relation, ch-replay-set, and ch-replay-map.

The term "transient" contrasts with "persistent".  I'm using the term "persistent" in its functional-data-structure sense, as Clojure does: a data structure is persistent if multiple states of it can coexist in memory efficiently.  (The probably more familiar use of the term is in the database sense, where it refers to nonvolatile storage of data.)  FSet collections have, up to now, all been persistent in this sense; a point modification to one, such as by with or less, takes only O(log n) space and time to return a new state of the collection, without disturbing the previous state.

A transient encapsulates the internal tree of a collection so as to guarantee that it holds the only pointer to the tree; this allows modifications to tree nodes to be made in-place, so long as the node has sufficient allocated space.  Once the collection is built, the tree is in the same format that existing FSet code expects, and can be accessed and functionally updated as usual.

Some quick micro-benchmarking suggests that speedups, for constructing a set from scratch, range from 1.6x at size 64 to as much as 2.4x at size 4096. 

You don't necessarily even have to use transients explicitly in order to benefit from them.  Some FSet builtins such as filter and image use them now.  The GMap result types ch-set etc. also use them.

For details, see the GitLab MR.

By Robert Smith

Fabrice Bellard came up with a computationally efficient formula for calculating the nth hexadecimal digit of $\pi$ without calculating any of the previous n−1. It’s called Bellard’s formula. It wasn’t the first of its kind, but in terms of computational efficiency, it was a substantial improvement over the original, elegant Bailey-Borwein-Plouffe formula. Due to the trio’s discovery, these formulas are often called BBP-type formulas.

Over the years, numerous BBP-type formulas have been discovered. In fact, Bailey gives us a recipe to search for them using integer-relation algorithms. In simple terms, we can just guess formulas, and run a computation to see if it likely equals $\pi$ with high confidence. If we do find one, then we can use it as a conjecture to prove formally.

Like Bellard and many others, I ran a variant of Bailey’s recipe, effectively doing a brute-force search, highly optimized and in parallel. The search yielded another formula that is computationally more efficient than Bellard’s formula. The identity is as follows:

$$ \pi = \sum_{k=0}^{\infty} \frac{1}{4096^k} \left( \frac{1}{6k+1} - \frac{2^{-5}}{6k+3} + \frac{2^{-8}}{6k+5} + \frac{2}{8k+1} - \frac{2^{-5}}{8k+5} + \frac{2^{-1}}{12k+3} - \frac{2^{-4}}{12k+7} - \frac{2^{-8}}{12k+11} \right). $$

It converges at a rate of 12 bits per term. We will prove convergence, and then prove the identity itself (with a little computer assistance). As it turns out, an equivalent form of this formula was already discovered, which we will discuss as well. Finally, we’ll show a very simple implementation in Common Lisp.

Proof of convergence

Write the series as $S := \sum_{k=0}^{\infty} 4096^{-k}R(k)$. Since $R(k)\in O(1/k)$, convergence is dominated by the geometric term $4096^{-k}$:

$$ \lim_{k \to \infty} \left\vert \frac{R(k+1)}{4096^{k+1}} \middle/ \frac{R(k)}{4096^{k}} \right\vert = \frac{1}{4096}. $$

By the ratio test, the series converges absolutely. Since $4096 = 2^{12}$, each additional term contributes exactly 12 bits of precision.

Bellard’s formula converges at 10 bits per term and requires the evaluation of 7 fractions. The above converges at 12 bits per term, and requires the evaluation of 8 fractions. So while we require 20% fewer terms, each term requires about 14% more arithmetic. So, net-net, this formula is approximately 5-6% more efficient.

Proof of identity via a definite integral

Consider $1/(nk+j) = \int_{0}^{1} x^{nk+j-1} dx$. For positive integers $n$ and $b$, we get

$$ \sum_{k=0}^{\infty} \frac{1}{b^k}\cdot\frac{1}{nk+j} = \sum_{k=0}^{\infty} \int_{0}^{1} \left(\frac{x^n}{b}\right)^k x^{j-1} dx. $$

We can swap the sum and integral via the Lebesgue dominated convergence theorem, since the power series $\sum (x^n/b)^k$ converges uniformly for $x \in [0, 1]$ and $b > 1$. Using this and summing the geometric series gives:

$$ \int_{0}^{1} x^{j-1} \sum_{k=0}^{\infty} \left(\frac{x^n}{b}\right)^k dx = \int_{0}^{1} \frac{x^{j-1}}{1 - x^n/b} dx. $$

We now apply this to $S$ termwise with $b=4096=2^{12}$:

$$ S = \int_0^1 \left( \frac{x^{0}}{1 - \frac{x^6}{2^{12}}} - 2^{-5} \frac{x^{2}}{1 - \frac{x^6}{2^{12}}} + 2^{-8} \frac{x^{4}}{1 - \frac{x^6}{2^{12}}} + 2 \frac{x^{0}}{1 - \frac{x^8}{2^{12}}} - 2^{-5} \frac{x^{4}}{1 - \frac{x^8}{2^{12}}} + 2^{-1} \frac{x^{2}}{1 - \frac{x^{12}}{2^{12}}} - 2^{-4} \frac{x^{6}}{1 - \frac{x^{12}}{2^{12}}} - 2^{-8} \frac{x^{10}}{1 - \frac{x^{12}}{2^{12}}} \right) dx. $$

At this point, you could try to algebra your way through, expanding, using the substitution $x=2u$, etc. ultimately yielding a nice denominator $(u^2\pm 2u+2)(u^6-64)(u^{12}-1)$. Maybe compute some residues. Or, just CAS your way through.

% fricas
FriCAS Computer Algebra System
Version: FriCAS 2025.12.23git built with sbcl 2.5.2.1852-1f3beec71
Timestamp: Wed Mar 4 12:41:38 EST 2026
-----------------------------------------------------------------------------
Issue )copyright to view copyright notices.
Issue )summary for a summary of useful system commands.
Issue )quit to leave FriCAS and return to shell.
-----------------------------------------------------------------------------
(1) -> f := (1/(1 - x^6/4096))
- (1/32)*x^2/(1 - x^6/4096)
+ (1/256)*x^4/(1 - x^6/4096)
+ 2*1/(1 - x^8/4096)
- (1/32)*x^4/(1 - x^8/4096)
+ (1/2)*x^2/(1 - x^12/4096)
- (1/16)*x^6/(1 - x^12/4096)
- (1/256)*x^10/(1 - x^12/4096);
Type: Fraction(Polynomial(Fraction(Integer)))
(2) -> normalize(integrate(f, x = 0..1))
3 1 11 19 1
(2) 2 atan(-) - 2 atan(-) + 2 atan(--) + 2 atan(--) + 2 atan(-)
2 2 24 48 4
Type: Expression(Fraction(Integer))

So now we just need to show the arctans all collapse to $\pi$. Recall the identity

$$ \tan^{-1} a \pm \tan^{-1} b = \tan^{-1}\left(\frac{a\pm b}{1\mp ab}\right). $$

The sum of the first four terms can be calculated easily in Common Lisp:

% sbcl --no-inform
* (defun combine (a b) (/ (+ a b) (- 1 (* a b))))
COMBINE
* (reduce #'combine '(3/2 -1/2 11/24 19/48))
4

So we have $2\big(\tan^{-1}4 + \tan^{-1}(1/4)\big)$, and with our final elementary trig identity $\tan^{-1} (a/b) = \pi/2 - \tan^{-1} (b/a)$, we find $S = \pi$.

A new discovery?

Of course, I was excited to find this formula, but after some internet spelunking, it turns out it had already been discovered by Géry Huvent and Boris Gourévitch, perhaps independently. Gourévitch doesn’t credit Huvent as he does with other formulas, but he does say “[…] furthermore, we can obtain BBP formula […] by using what Gery Huvent calls the denomination tables […].” Daisuke Takahashi cites Huvent’s website in this 2019 paper published in The Ramanujan Journal. In all cases, they write the formula in the following way:

$$ \frac{1}{128} \sum _{k=0}^{\infty} \frac{1}{2^{12k}}\left( \frac{768}{24 k+3}+\frac{512}{24k+4}+\frac{128}{24 k+6}-\frac{16}{24 k+12}-\frac{16}{24 k+14}-\frac{12}{24 k+15}+\frac{2}{24 k+20}-\frac{1}{24 k+22}\right), $$

which is structurally equivalent to $S$.

Despite having been known already, this formula doesn’t appear to be well known. As such, I hope this blog post brings more attention to it.

Simple implementation

Here is a simple implementation of digit extraction using BBP-type formulas in Common Lisp:

(defun %pow2-mod (exponent modulus)
(cond
((= modulus 1) 0)
((zerop exponent) 1)
(t
(let ((result 1)
(base (mod 2 modulus))
(e exponent))
(loop :while (plusp e) :do
(when (oddp e)
(setf result (mod (* result base) modulus)))
(setf base (mod (* base base) modulus)
e (ash e -1)))
result))))
(defun %scaled-frac-of-power-two (exponent denom)
(cond
((>= exponent 0)
(let ((residue (%pow2-mod exponent denom)))
(floor (ash residue *precision-bits*) denom)))
(t
(let ((effective-bits (+ *precision-bits* exponent)))
(if (minusp effective-bits)
0
(floor (ash 1 effective-bits) denom))))))
(defun %series-scaled-frac (bit-index bbp-series k-step global-shift alternating-p)
;; A series is a list of series terms. A series term is a quadruple
;; (SIGN SHIFT DENOM-MULTIPLIER DENOM-OFFSET) representing the summand
;; SIGN * 2^SHIFT / (DENOM_MULTIPLIER * k + DENOM_OFFSET).
(let* ((modulus (ash 1 *precision-bits*))
(max-shift (loop :for term :in bbp-series :maximize (second term)))
(k-max (max 0 (ceiling (+ bit-index ; conservative bound
global-shift
max-shift
*precision-bits*
*guard-bits*)
k-step))))
(loop :with acc := 0
:for k :from 0 :to k-max :do
(let ((k-sign (if (and alternating-p (oddp k)) -1 1))
(k-factor (* k-step k)))
(dolist (term bbp-series)
(destructuring-bind (term-sign shift den-mul den-add) term
(let* ((denom (+ den-add (* den-mul k)))
(exponent (+ bit-index global-shift shift (- k-factor)))
(piece (%scaled-frac-of-power-two exponent denom))
(signed (* k-sign term-sign)))
(when (plusp piece)
(setf acc (mod (+ acc (* signed piece)) modulus)))))))
:finally (return acc))))
(defun %nth-hex-from-series (n terms k-step global-shift alternating-p)
(let* ((bit-index (* 4 n)))
(ldb (byte 4 (- *precision-bits* 4))
(%series-scaled-frac bit-index
terms
k-step
global-shift
alternating-p))))

This implementation uses Lisp’s arbitrary precision integer arithmetic. A “real” implementation would use more efficient arithmetic, but this will suffice for some basic testing. Now we can write functions to use the Bellard formula and the new formula:

(defparameter +bellard-terms+
'((-1 5 4 1)
(-1 0 4 3)
(+1 8 10 1)
(-1 6 10 3)
(-1 2 10 5)
(-1 2 10 7)
(+1 0 10 9)))
(defun bellard-nth-hex (n)
(%nth-hex-from-series (* 4 n) +bellard-terms+ 10 -6 t))
(defparameter +new-terms+
'((+1 0 6 1)
(-1 -5 6 3)
(+1 -8 6 5)
(+1 1 8 1)
(-1 -5 8 5)
(+1 -1 12 3)
(-1 -4 12 7)
(-1 -8 12 11)))
(defun new-nth-hex (n)
(%nth-hex-from-series (* 4 n) +new-terms+ 12 0 nil))

Let’s make sure they agree for the first 1000 hex digits:

CL-USER> (loop :for i :below 1000
:always (= (bellard-nth-hex i) (new-nth-hex i)))
T

And now let’s look at timing comparisons. Here’s a little driver:

(defun compare-timings (n)
(flet ((time-it (f n)
(sb-ext:gc :full t)
(let ((start (get-internal-real-time)))
(funcall f n)
(- (get-internal-real-time) start))))
(loop :repeat n
:for index := 1 :then (* 10 index)
:for bellard := (time-it #'bellard-nth-hex index)
:for new := (time-it #'new-nth-hex index)
:do (format t "~v,' D: new is ~A% faster than bellard~%" n index
(round (* 100 (- bellard new)) bellard)))))

And the results if the timing up to the one millionth hexadecimal digit:

CL-USER> (compare-timings 7)
1 : new is 81% faster than bellard
10 : new is 7% faster than bellard
100 : new is 6% faster than bellard
1000 : new is 5% faster than bellard
10000 : new is 4% faster than bellard
100000 : new is 3% faster than bellard
1000000: new is 4% faster than bellard

As predicted, though imperfect a test, it’s consistently faster across a few orders of magnitude.

Contents

• Part 1 (Hello World)
• Part 2 (Basic Templates)
• Part 3 (Introduction to middleware and Static File management)
• Part 4 (Forms)
• Part 5 (Environmental Variables)
• Part 6 (Database Connections)
• Part 7 (Envy Configuation Switching)
• Part 8 (Mounting Middleware)
• Part 9 (Authentication System)
• Part 10 (Email)
• Part 11 (Posting Tweets & Advanced Database Queries)
• Part 12 (Clean Up & Bug Fix)
• Part 13 (Adding Comments)
• Part 14 (Pagination, Part 1)
• Part 15 (Pagination, Part 2)

Introduction

Welcome back! We will be revisiting the pagination from last time, however we are going to try and make this easier on ourselves, I built a package for pagination mito-pager, the idea is that much of what we looked at in the last lesson was very boiler plate and repetitive so we should look at removing this.

I will say, my mito-pager can do a little more than just what I show here, it has two modes, you can use paginate-dao (named this way so that it is familiar to mito) to paginate over simple models, however, if you need to perform complex queries there is a macro with-pager that you can use to paginate. It is this second form we will use in this tutorial.

There is one thing to bear in mind, when using mito-pager, you must implement your data retrieval functions in such a way to return a values object, as mito-pager relies on this to work.

I encourge you to try the library out in other use-cases and, of course, if you have ideas, please let me know.

Changes

Most of our changes are quite limited in scope, really it's just our controllers and models that need most of the edits.

ningle-tutorial-project.asd

We need to add the mito-pager package to our project asd file.

- :ningle-auth)
+ :ningle-auth
+ :mito-pager)

src/controllers.lisp

Here is the real payoff! I almost dreaded writing the sheer volume of the change but then realised it's so simple, we only need to change our index function, and it may be better to delete it all and write our new simplified version.

(defun index (params)
  (let* ((user (gethash :user ningle:*session*))
         (req-page (or (parse-integer (or (ingle:get-param "page" params) "1") :junk-allowed t) 1))
         (req-limit (or (parse-integer (or (ingle:get-param "limit" params) "50") :junk-allowed t) 50)))
    (flet ((get-posts (limit offset) (ningle-tutorial-project/models:posts user :offset offset :limit limit)))
      (mito-pager:with-pager ((posts pager #'get-posts :page req-page :limit req-limit))
        (djula:render-template* "main/index.html" nil :title "Home" :user user :posts posts :pager pager)))))

This is much nicer, and in my opinion, the controller should be this simple.

src/main.lisp

We need to ensure we include the templates from mito-pager, this is a simple one line change.

 (defun start (&key (server :woo) (address "127.0.0.1") (port 8000))
    (djula:add-template-directory (asdf:system-relative-pathname :ningle-tutorial-project "src/templates/"))
+   (djula:add-template-directory (asdf:system-relative-pathname :mito-pager "src/templates/"))

src/models.lisp

As mentioned at the top of this tutorial, we have to implement our data retrieval functions in a certain way. While there are some changes here, we ultimately end up with less code.

We can start by removing the count parameter, we wont be needing it in this implementation, and since we don't need the count parameter anymore, the :around method can go too!

- (defgeneric posts (user &key offset limit count)
+ (defgeneric posts (user &key offset limit)
-
- (defmethod posts :around (user &key (offset 0) (limit 50) &allow-other-keys)
-   (let ((count (mito:count-dao 'post))
-         (offset (max 0 offset))
-         (limit (max 1 limit)))
-     (if (and (> count 0) (>= offset count))
-       (let* ((page-count (max 1 (ceiling count limit)))
-              (corrected-offset (* (1- page-count) limit)))
-         (posts user :offset corrected-offset :limit limit))
-       (call-next-method user :offset offset :limit limit :count count))))

There's two methods to look at, the first is when the type of user is user:

-
- (defmethod posts ((user user) &key offset limit count)
+ (defmethod posts ((user user) &key offset limit)
...
      (values
-         (mito:retrieve-by-sql sql :binds params)
-         count
-         offset)))
+         (mito:retrieve-by-sql sql :binds params)
+         (mito:count-dao 'post))))

The second is when the type of user is null:

-
- (defmethod posts ((user null) &key offset limit count)
+ (defmethod posts ((user null) &key offset limit)
...
    (values
-       (mito:retrieve-by-sql sql)
-       count
-       offset)))
+       (mito:retrieve-by-sql sql)
+       (mito:count-dao 'post))))

As you can see, all we are really doing is relying on mito to do the lions share of the work, right down to the count.

src/templates/main/index.html

The change here is quite simple, all we need to do is to change the path to the partial, we need to simply point to the partial provided by mito-pager.

- {% include "partials/pager.html" with url="/" title="Posts" %}
+ {% include "mito-pager/partials/pager.html" with url="/" title="Posts" %}

src/templates/partials/pagination.html

This one is easy, we can delete it! mito-pager provides its own template, and while you can override it (if you so wish), in this tutorial we do not need it anymore.

Conclusion

I hope you will agree that this time, using a prebuilt package takes a lot of the pain out of pagination. I don't like to dictate what developers should, or shouldn't use, so that's why last time you were given the same information I had, so if you wish to build your own library, you can, or if you want to focus on getting things done, you are more than welcome to use mine, and of course, if you find issues please do let me know!

Learning Outcomes

Github

• The link for the custom pagination part of the tutorials code is available here.

Common Lisp HyperSpec

If you have a unary function F, you can compose it with function G, H = F ∘ G, which means H(x) = F(G(x)). Instead of running x through F directly, you run it through G first and then run the output of G through F.

If F is a binary function, then you either compose it with a unary function G on the left input: H = F ∘_left G, which means H(x, y) = F(G(x), y) or you compose it with a unary function G on the right input: H = F ∘_right G, which means H(x, y) = F(x, G(y)).

(binary-compose-left f g)  = (λ (x y) (f (g x) y))
(binary-compose-right f g) = (λ (x y) (f x (g y)))

We could extend this to trinary functions and beyond, but it is less common to want to compose functions with more than two inputs.

binary-compose-right comes in handy when combined with fold-left. This identity holds

 (fold-left (binary-compose-right f g) acc lst) <=>
   (fold-left f acc (map g lst))

but the right-hand side is less efficient because it requires an extra pass through the list to map g over it before folding. The left-hand side is more efficient because it composes g with f on the fly as it folds, so it only requires one pass through the list.

I released a hopefully inspiring gallery:

lisp-screenshots.org

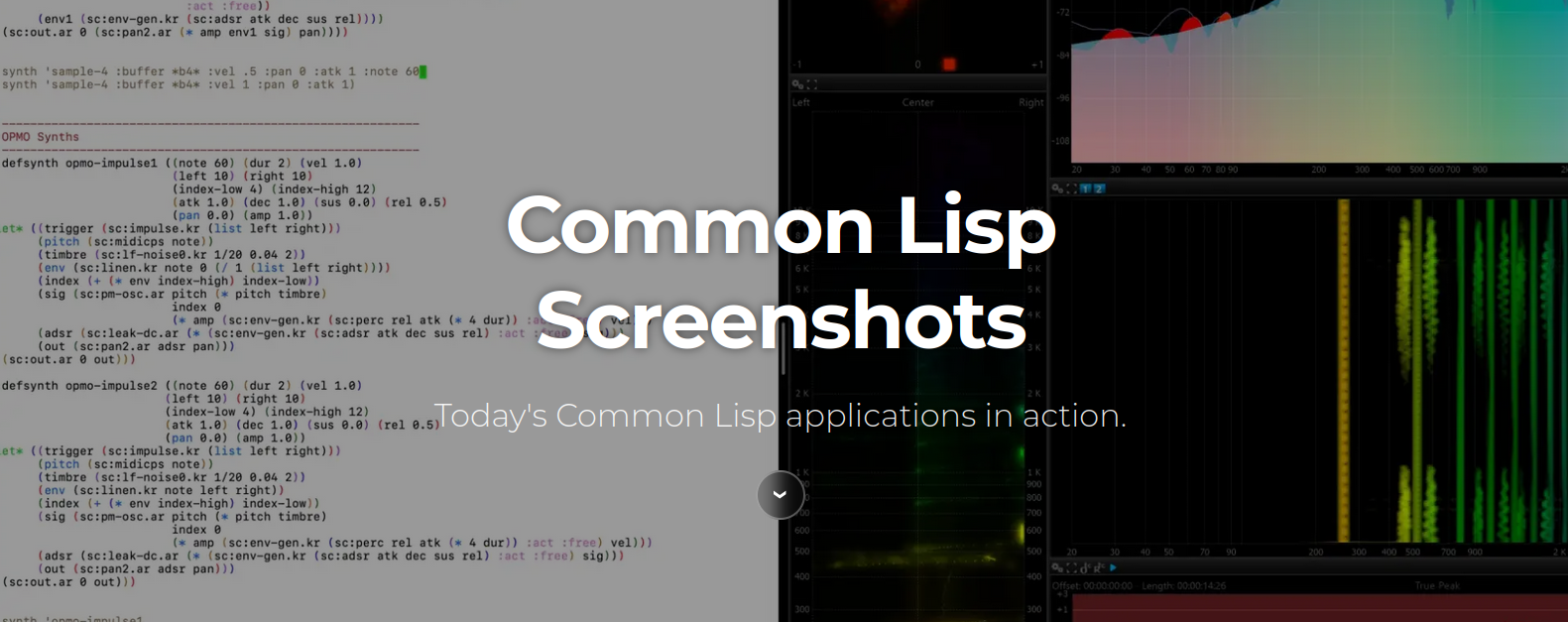
We divide the showcase under the categories Music, Games, Graphics and CAD, Science and industry, Web applications, Editors and Utilities.

Of course:

“Please don’t assume Lisp is only useful for...

thank you ;)

For more example of companies using CL in production, see this list (contributions welcome, of course).

Don’t hesitate to share a screenshot of your app! It can be closed source and yourself as the sole user, as long as it as some sort of a GUI, and you use it. Historical success stories are for another collection.

The criteria are:

• built in Common Lisp
• with some sort of a graphical interface
• targeted at end users
• a clear reference, anywhere on the web, by email to me or simply as a comment here, that it is built in CL.

Details:

• it can be web applications whose server side is CL, even if the JS/HTML is classical web tech.
• no CLI interfaces. A readline app is OK but hey, we can do better.
• it can be closed-source or open-source, commercial, research or a personal software
• regarding “end users”: I don’t see how to include a tool like CEPL, but I did include a screen of LispWorks.
• bonus point if it is developed in a company (we want it on https://github.com/azzamsa/awesome-lisp-companies/), be it a commercial product or an internal tool.

You can reach us on GitHub discussions, by email at (reverse "gro.zliam@stohsneercs+leradniv") and in the comments.

Best,

Mark Friedman just released his Scheme-JS interpreter which is a Scheme with transparent JavaScript interoperability. See his blog post at furious ideas.

This interpreter apparently uses the techniques of lightweight stack inspection — Mark consulted me a bit about that hack works. I'm looking forward to seeing the vibe coded architecture.

Classical literate programming

A literate program intersperses narrative and code chunks. From this, source code to be fed to the compiler is generated by a process called tangling, and documentation by weaving. The specifics of tangling vary, but by allowing complete reordering and textual combination of chunks, it lets the human narrative drive the exposition at the cost of introducing an additional step into the write-compile-run cycle.

The general idea

It is easy to mistake this classical implementation of literate programming for the more general idea that we want to

1. present code to human readers in pedagogical order with narrative added, and

2. make changing code and its documentation together easy.

The advantages of literate programming follow from these desiderata.

Untangled LP

In many languages today, code order is far more flexible than in the era of early literate programming, so the narrative order can be approximated to some degree using docstrings and comments. Code and its documentation are side by side, so changing them together should also be easy. Since the normal source code now acts as the LP source, there is no more tangling in the programming loop. This is explored in more detail here.

Pros and cons

Having no tangling is a great benefit, as we get to keep our usual programming environment and tooling. On the other hand, bare-bones untangled LP faces the following potential problems.

1. Order mismatch: Things like inline functions and global variables may need to be defined before use. So, code order tends to deviate from narrative order to some degree.

2. Reduced locality: Our main tool to sync code and narrative is factoring out small, meaningful functions, which is just good programming style anyway. However, this may be undesirable for reasons of performance or readability. In such a case, we might end up with a larger function. Now, if we have only a single docstring for it, then it can be non-obvious which part of the code a sentence in the docstring refers to because of their distance and the presence of other parts.

3. No source code only view: Sometimes we want to see only the code. In classical LP, we can look at the tangled file. In untangled LP, editor support for hiding the narrative is the obvious solution.

4. No generated documentation: There is no more tangling nor weaving, but we still need another tool to generate documentation. Crucially, generating documentation is not in the main programming loop.

In general, whether classical or untangled LP is better depends on the severity of the above issues in the particular programming environment.

The Lisp and PAX view

MGL-PAX, a Common Lisp untangled LP solution, aims to minimize the above problems and fill in the gaps left by dropping tangling.

1. Order

   • Common Lisp is quite relaxed about the order of function definitions, but not so much about DEFMACRO, DEFVAR, DEFPARAMETER, DEFCONSTANT, DEFTYPE , DEFCLASS, DEFSTRUCT, DEFINE-COMPILER-MACRO, SET-MACRO-CHARACTER, SET-DISPATCH-MACRO-CHARACTER, DEFPACKAGE. However, code order can for the most part follow narrative order. In practice, we end up with some DEFVARs far from their parent DEFSECTIONs (but DECLAIM SPECIAL helps).

   • DEFSECTION controls documentation order. The references to Lisp definitions in DEFSECTION determine narrative order independently from the code order. This allows the few ordering problems to be patched over in the generated documentation.

   • Furthermore, because DEFSECTION can handle the exporting of symbols, we can declare the public interface piecemeal, right next to the relevant definitions, rather than in a monolithic DEFPACKAGE

2. Locality

   • Lisp macros replace chunks in the rare, complex cases where a chunk is not a straightforward text substitution but takes parameters. Unlike text-based LP chunks, macros must operate on valid syntax trees (S-expressions), so they cannot be used to inject arbitrary text fragments (e.g. an unclosed parenthesis).

     This constraint forces us to organize code into meaningful, syntactic units rather than arbitrary textual fragments, which results in more robust code. Within these units, macros allow us to reshape the syntax tree directly, handling scoping properly where text interpolation would fail.

   • PAX's NOTE is an extractable, named comment. NOTE can interleave with code within e.g. functions to minimize the distance between the logic and its documentation.

   • Also, PAX hooks into the development to provide easy navigation in the documentation tree.

3. Source code only view: PAX supports hiding verbose documentation (sections, docstrings, comments) in the editor.

4. Generating documentation

   • PAX extracts docstrings, NOTEs and combines them with narrative glue in DEFSECTIONs.

   • Documentation can be generated as static HTML/PDF files for offline reading or browsed live (in an Emacs buffer or via an in-built web server) during development.

   • LaTeX math is supported in both PDF and HTML (via MathJax, whether live or offline).

Zach Beane has released the latest Quicklisp beta (January 2026), and I am pleased to have contributed to this release. Here are the highlights:

• dual-numbers — Implements dual numbers and automatic differentiation using dual numbers for Common Lisp.
• fold — FOLD-LEFT and FOLD-RIGHT functions.
• function — Provides higher-order functions for composition, currying, partial application, and other functional operations.
• generic-arithmetic — Defines replacement generic arithmetic functions with CLOS generic functions making it easier to extend the Common Lisp numeric tower to user defined numeric types.
• named-let — Overloads the LET macro to provide named let functionality similar to that found in Scheme.

Selected Functions

Dual numbers

(defun square (x) (* x x))

(let ((df (derivative #'square)))
  (funcall df 5)) 
;; => 10
    

Function

;; Summing the squares of a list
(fold-left (binary-compose-right #'+ #'square) 0 '(1 2 3))
;; => 14  ; (+ (+ (+ 0 (sq 1)) (sq 2)) (sq 3))
    

FOLD

(fold-left (lambda (acc x) (cons x acc))
           nil
           '(1 2 3))
;; => (3 2 1)  ; Effectively reverses the list
    

Named Let

;; Standard Countdown Loop
(let recur ((n 10))
  (if (zerop n)
      'blastoff
      (progn
        (print n)
        (recur (1- n)))))
    

Contents

• Part 1 (Hello World)
• Part 2 (Basic Templates)
• Part 3 (Introduction to middleware and Static File management)
• Part 4 (Forms)
• Part 5 (Environmental Variables)
• Part 6 (Database Connections)
• Part 7 (Envy Configuation Switching)
• Part 8 (Mounting Middleware)
• Part 9 (Authentication System)
• Part 10 (Email)
• Part 11 (Posting Tweets & Advanced Database Queries)
• Part 12 (Clean Up & Bug Fix)
• Part 13 (Adding Comments)
• Part 14 (Pagination, Part 1)
• Part 15 (Pagination, Part 2)

Introduction

Hello and welcome back, I hope you all had a good festive season, I took a break last month as I usually get very busy in December, but lest you think I had stopped posting, I have prepared a two part lesson this time: Pagination. We are first going to look at rolling your own pagination, but we will then look at integrating a package I wrote ningle-pager, to simplify the code. This way if my package doesn't fit your needs, you have the information required to build your own solution.

In practical terms, something like a microblogging app would use infinite scrolling, but we don't have anywhere enough data to present that as a lesson right now, and besides pagination has a lot of uses, Google and Amazon use it for their products, so it must be pretty useful!

Theory

In SQL, there is the ability to LIMIT results, but also, the ability to start from an OFFSET, which ultimately does the heavy lifting for us. We have previously looked at SXQL, which is a thin layer upon SQL, so we can use (limit 50) and (offset 100) (or whatever values we want) to interact with the database, we will also use GET parameters like ?page=2&limit=50 (or something). So with this information we know the url patterns and we know what SXQL forms we want to use, we just have to design how our application will work internally.

Our solution will define an interface, any controller that needs to be paginated will:

• Accept a page keyword parameter
• Accept a limit keyword parameter
• Return a values list that has 3 items, the results, the total count, and the offset.

The work will touch the models, the controllers, and the templates:

Models

We are gonna get deep into the weeds with clos in how we implement our pagination in this part, there's multiple methods so we will take each implementation one by one. You can learn more about how OOP is implemented in my older videos.

generic Method

We start with a generic definition, we already had one, but we are modifying it. Fun fact, the generic method defines all the parameters a method might use, but not all methods must use the arguments, which comes in real handy for us later:

(defgeneric posts (user &key offset limit count)
  (:documentation "Gets the posts"))

Here we have a generic method, generic methods do nothing on their own, they help us define what a method should do, but of course under certain circumstances how a method does what it does may need to change, this allows us to implment different specialised concrete methods, we will look at this below.

What we have done with this generic method is add key arguments offset, limit, and count, as we saw previously, all this does is declare a :documentation form.

:around method

As you may, or may not know, the Common Lisp Object System (clos for short) allows us to define, as we have done previously primary methods, these are methods that specialise on one (or more) of the parameters. When passed arguments at the point the method is called, the method matching the parameter type of the arguments passed will trigger. That is why our posts method specifies user to be a user object, or null and handles the logic in different ways. It also allows us to define auxiliary methods, which are known as :before, :after, and :around. The :before methods will run, well, before the related primary method is called, with each :before method being called by its most specific signature to its least. :after methods are the total opposite, they run after a primary method is run, and they run from the least specific version to the most specific. They would be where we might want to add signals, or logging, we could have a :before, and :after around the mito:save-dao that we use and the :before method sends a pre-save signal while the :after sends a post-save signal.

It is not, however the :before/:after methods we care about here, we in fact will write an :around, which is a more fundamental building block. :around methods control, how, when, or even if, a primary method gets called, the other methods can't control this. As previously discussed they have a specific order in which they run, so if we wanted to... say... capture arguments and do some processing on them because, I dunno, we should never trust user input, prior to running our primary method, an :around method is what we would need to use.

The real "magic" of how to do what we want to do is use an :around method. We will look at the complete implementation a little bit later, but we need to pause and ensure we really understand about method combination in Common Lisp.

As we mentioned in the defgeneric, not every method needs to use or specialise on every parameter, and in this :around method you will notice that the count is absent, that is by design, because the :around method will compute it and pass it onto the next method in the chain, instead it uses &allow-other-keys to allow these key arguments to be accepted, but also since they are unnamed, the compiler won't emit a warning that they're not used.

Our implementation is here:

(defmethod posts :around (user &key (offset 0) (limit 50) &allow-other-keys)
  (let ((count (mito:count-dao 'post))
        (offset (max 0 offset))
        (limit (max 1 limit)))
    (if (and (> count 0) (>= offset count))
      (let* ((page-count (max 1 (ceiling count limit)))
             (corrected-offset (* (1- page-count) limit)))
        (posts user :offset corrected-offset :limit limit))
      (call-next-method user :offset offset :limit limit :count count))))

The first thing to note is the obvious :around keyword that comes after the posts name, this is how we declare a method as an :around method. The next thing to notice is that the count parameter is not declared, instead we use the &allow-other-keys, as discussed above. This method will modify some variables or recalculate the offset if it was invalid before either calling itself (to perform the recalculations) or call the next method with, well, call-next-method.

We begin with a let form that will get the number of items by using mito:count-dao, we determine the offset by getting the max of 0 or the offset, we also define limit as the max of 1 and limit.

The key check here is in the if form, which checks that both the count is larger than zero (> count zero) and the offset is bigger than the count (>= offset count), this tells us that an invalid condition exists, we can't request an offset to be larger than the number of items, so we have to handle it. Under these circumstances we need to get the new page-count by calculating (max 1 (ceiling count limit)), this will round up the result of dividing count by limit, and returns that, or 1.

Once we have that we can calculate a corrected offset by using the formula (* (1- page-count) limit), to run through how this formula works, here are some examples, if we assume limit is defined as 50, we can increment the page-count by one each time to see how this calculation works:

• Page 1: (* (1- 1) 50) -> (* 0 50) -> 0
• Page 2: (* (1- 2) 50) -> (* 1 50) -> 50
• Page 3: (* (1- 3) 50) -> (* 2 50) -> 100

With this calculation done we can recursively call the method again, this time with the correct values, which brings us to our base case, calling the next method via call-next-method with the appropriate values which handily brings us to the specific methods now. We can actually dramatically simplify our primary methods thanks to the :around method.

Something to bear in mind, our count here is real easy, cos we are just returning all posts, but a more complex application may need more complex logic to determine what and how you are counting.

user method

Since we don't need to handle any error state or recovery (because the :around method handles it), we can actually write simple methods that perform a query and return the results. We have also simplified the way in which we run queries, turns out the sxql:yield returns multiple values, the first is the SQL string, the second is a list of params to be spliced into it (to avoid sql injection attacks), so we set up a multiple-value-bind form to capture these, and we put our SQL together, we previously used :? which was fine, as that is the character used to be a place holder, but this way is nicer to write. The things you learn, eh?

Please note however, where in our :around method we didn't specify the count parameter that the generic method defines, in this primary method, we do!

All we do it use a values form to return the result of running the sql, with the parameters bound to it, the count (number of items total) and the offset from where it starts returning results from.

(defmethod posts ((user user) &key offset limit count)
  (multiple-value-bind (sql params)
        (sxql:yield
              (sxql:select
                  (:post.*
                    (:as :user.username :username)
                    (:as (:count :likes.id) :like_count)
                    (:as (:count :user_likes.id) :liked_by_user))
                  (sxql:from :post)
                  (sxql:left-join :user :on (:= :post.user_id :user.id))
                  (sxql:left-join :likes :on (:= :post.id :likes.post_id))
                  (sxql:left-join (:as :likes :user_likes)
                                  :on (:and (:= :post.id :user_likes.post_id)
                                            (:= :user_likes.user_id (mito:object-id user))))
                  (sxql:group-by :post.id)
                  (sxql:order-by (:desc :post.created_at))
                  (sxql:offset offset)
                  (sxql:limit limit)))
      (values
          (mito:retrieve-by-sql sql :binds params)
          count
          offset)))

This makes our primary method much tighter, it runs a query and returns results, the :around method handles the recalculation logic (which is shared between this primary method and the next). Nice and simple.

null method

So having seen the form of our new primary methods above, we follow the same patern for the primary method where the user is null. As before this primary method accepts the count parameter.

(defmethod posts ((user null) &key offset limit count)
  (multiple-value-bind (sql)
      (sxql:yield
        (sxql:select
            (:post.*
              (:as :user.username :username)
              (:as (:count :likes.id) :like_count))
            (sxql:from :post)
            (sxql:left-join :user :on (:= :post.user_id :user.id))
            (sxql:left-join :likes :on (:= :post.id :likes.post_id))
            (sxql:group-by :post.id)
            (sxql:order-by (:desc :post.created_at))
            (sxql:limit limit)
            (sxql:offset offset)))
    (values
        (mito:retrieve-by-sql sql)
        count
        offset)))

The query is simpler, and we do not need to actually pass any variables into the SQL string, so we don't need the params value returned from the multiple-value-bind, which means we also don't need to use the :binds key argument into mito:retrieve-by-sql.

And that's it, that's our models done!

Controllers

Our controller will be the index controller we built previously, but we need to modify it quite a bit to parse and process the information we need, pagination has a lot of data, and we will need to ensure our templates can present the UI and data in a easy to use manner.

The controller will be so radically different as to be entirely new, it may be easier for you to delete the existing index controller and replace it with what we write here.

The first thing the controller needs to do is grab the GET parameters and validate them, we follow a basic formula to achieve this for the two parameters we need (page, and limit):

(or (parse-integer (or (ingle:get-param "page" params) "1") :junk-allowed t) 1)
(or (parse-integer (or (ingle:get-param "limit" params) "50") :junk-allowed t) 50)

As you can see these are basically identical the only thing that differs are the default values, in the case of page it is "1"/1 for limit it is "50"/50. To run through the logic we have some basic possibilities we need to handle.

In the case where there is no parameter which will be the case if no page=x is in url, or the value of page is not numeric (such as a word, page=hi or something) the result of (ingle:get-param "page" params) will be nil.

In the case where page is provided and is a number, the process is the same, but (ingle:get-param "page" params) would return a number as a string.

We can see how that would evaluate here:

(or (parse-integer (or (ingle:get-param "page" params) "1") :junk-allowed t) 1)
(or (parse-integer (or nil "1") :junk-allowed t) 1)
(or (parse-integer "1" :junk-allowed t) 1)
(or 1 1)
1

The process repeats for the "limit" parameter. It's a lot of checking and handling, it would be nice if there were a library to handle this for us, but I have not yet found one, perhaps that will be our next topic!

NOTE! In this example we are permitting arbitrary limit values (we are learning), in practice, this should be limited to a maximum value to prevent users from requesting a page that may result in a Denial Of Service type event. What the exact value should be really depends on the data, it might be fine to get thousands of numbers in one go, but if your models are complicated, a smaller number may be better.

You could do something like this to limit... the limit: (limit (min 100 (max 1 limit)))

The let binding will therefore look like this

(let ((user (gethash :user ningle:*session*))
      (page (or (parse-integer (or (ingle:get-param "page" params) "1") :junk-allowed t) 1))
      (limit (or (parse-integer (or (ingle:get-param "limit" params) "50") :junk-allowed t) 50)))
  ...)

With those parameters validated, we can focus on building our paginated controller. Thanks to the work we did in the models we can pull the values out of the posts method with multiple-value-bind:

(let ((user (gethash :user ningle:*session*))
      (page (or (parse-integer (or (ingle:get-param "page" params) "1") :junk-allowed t) 1))
      (limit (or (parse-integer (or (ingle:get-param "limit" params) "50") :junk-allowed t) 50)))
  (multiple-value-bind (posts count offset) (ningle-tutorial-project/models:posts user :offset (* (1- page) limit) :limit limit)
    ...))

This enables us to now calculate the various values we need to pass through into a template to render the paginator, we need to generate 6 values.

page

The page variable is a way to determine what the current page is, it is calculated like so:

(1+ (floor offset limit))

From the offset we get from the multiple-value-bind we round down the value of dividing offset by the limit and add 1 to the value. If we assume, for example, an offset of 50 and a limit of 50, we can see how the page is determined.

(1+ (floor 50 50))
(1+ 1)
2

If we want to see something larger:

(1+ (floor 250 50))
(1+ 5)
6

page count

The page-count variable is a way to determine the total number of pages:

(max 1 (ceiling count limit))

Again, from the multiple-value-bind we get the count object, so we can expand this, assuing count is 250 and limit is 50.

(max 1 (ceiling 500 50))
(max 1 10)
10

In this manner, given a total number and a page size we want to split it into, we can see the total number of pages.

previous page number

Unlike the previous two calculations, prev-page can legitiately be nil. In the case we are already on the first page there's no way for there to be a previous page, so nil is fine. If we need to have some binary conditional logic where nil is acceptable when is our friend.

(when (> page 1) (1- page))

Wwhen the page is bigger than one, return one less than the value of page, because this is a when (1- page) will be returned, or nil will be.

page number

The inverse of the above:

(when (< page page-count) (1+ page))

When the page is smaller than the total number of pages, return one more than the value of page, or nil.

range start

Range start is to help the UI, typically in paginators, especially in large ones, there's a first, last, and current location, but often the current location has some pages to the left and right, this is the range. Now there's no real right number for the ranges, but I settled on 2.

(max 1 (- page 2))

Assuming page is 1, max will return 1, but if we are on, say, page 15, the location the range starts at is 13.

range end

Range end behaves like range start, except in the other direction, but we need to ensure we get the minimum of the page-count, in case we are on the last page.

(min page-count (+ page 2))

With these defined we can put them in a let* form.

(let ((user (gethash :user ningle:*session*))
      (page (or (parse-integer (or (ingle:get-param "page" params) "1") :junk-allowed t) 1))
      (limit (or (parse-integer (or (ingle:get-param "limit" params) "50") :junk-allowed t) 50)))
  (multiple-value-bind (posts count offset) (ningle-tutorial-project/models:posts user :offset (* (1- page) limit) :limit limit)
    (let* ((page (1+ (floor offset limit)))
           (page-count (max 1 (ceiling count limit)))
           (prev-page (when (> page 1) (1- page)))
           (next-page (when (< page page-count) (1+ page)))
           (range-start (max 1 (- page 2)))
           (range-end (min page-count (+ page 2))))
        ...)))

The final thing we need to do is return the result of djula:render-template*, but there is still more data we need to pass through, build upon the variables we defined, there's only 5 more.

pages

Pages is simply a list of all the pages, which is easy enough to generate:

(loop :for idx :from range-start :to range-end :collect idx)

show-start-gap

The show-start-gap is a boolean that tells the template to render part of the paginator UI.

(> range-start 2)

This will return t or nil depending on if range-start is larger than 2.

show-end-gap

The show-end-gap is the inverse:

(< range-end (1- page-count))

This will return t or nil depending on if range-end is smaller than (1- page-count).

start-index

To get the start-index, this is the number starting from the offset so we can display something like "Showing x - y of z", x would be our start-index.

(if (> count 0) (1+ offset) 0)

If the count is bigger than zero then we return one more than the offset, else we return 0 (the default starting offset being 0).

end-index

Again, this is the opposite of another thing, the start-index.

(if (> count 0) (min count (+ offset (length posts))) 0)

If count is bigger than zero then what we need is the smallest (min) of the count and offset plus the number of posts, or 0. It's possible there isn't a complete pages worth of items, so we need to ensure that we don't over run.

With all that being said, we can now see the complete controller with the values rendered by djula:

(defun index (params)
    (let ((user (gethash :user ningle:*session*))
          (page (or (parse-integer (or (ingle:get-param "page" params) "1") :junk-allowed t) 1))
          (limit (or (parse-integer (or (ingle:get-param "limit" params) "50") :junk-allowed t) 50)))
      (multiple-value-bind (posts count offset) (ningle-tutorial-project/models:posts user :offset (* (1- page) limit) :limit limit)
        (let* ((page (1+ (floor offset limit)))
               (page-count (max 1 (ceiling count limit)))
               (prev-page (when (> page 1) (1- page)))
               (next-page (when (< page page-count) (1+ page)))
               (range-start (max 1 (- page 2)))
               (range-end (min page-count (+ page 2))))
          (djula:render-template*
            "main/index.html"
            nil
            :title "Home"
            :user user
            :posts posts
            :form (if user (cl-forms:find-form 'post) nil)
            :count count
            :page page
            :limit limit
            :page-count page-count
            :prev-page prev-page
            :next-page next-page
            :pages (loop :for idx :from range-start :to range-end :collect idx)
            :show-start-gap (> range-start 2)
            :show-end-gap (< range-end (1- page-count))
            :start-index (if (> count 0) (1+ offset) 0)
            :end-index (if (> count 0) (min count (+ offset (length posts))) 0))))))

I would have thought that having an invalid number would have triggered a 404, or perhaps a 400, but having tested this with Google, it seems that the convention is to default to page 1. So with that said and the controller in place, we can now write our templates.

Templates

index (src/templates/main/index.html)

Our index template doesn't require much change at all, we need to only add an include (from djula) to include the contents of one template inside another. Of course we have still to write the pagination template, but that is just below.

 {% extends "base.html" %}

{% block content %}
 <div class="container">
    <!-- Post form -->
    <div class="row mb-4">
        <div class="col">
            {% if form %}
                {% form form %}
            {% endif %}
        </div>
    </div>

    <!-- Posts Section -->
+   {% include "partials/pagination.html" with url="/" title="Posts" %}
    <div class="row">
    ...
    </div>
+   {% include "partials/pagination.html" with url="/" title="Posts" %}
 </div>
 {% endblock %}

Something to bear in mind here is the way this is designed is that if you need to pass in some data, in our case url, and title, we can pass through these things, we will use these in the pagination html partial.

pagination (src/templates/partials/pagination.html)

Partials are a way to include reusable parts of html presentation in a template, they help us build isolated pieces of presentation logic that we might want to use over and over again all over our application, this is why we save them in a partials folder, because they are a partial piece of presentation logic.

This is the magic that makes the UI work, while we showed were it would be used in the index.html page, we need to look into what it does. I do use bootstrap to make things look nice, but I'm very much NOT a frontend engineer, so I can't speak to how to make something look good without it, so inevitably much of the classes and UI come from Bootstrap.

I will have to break the html down piece by piece to explain what it's all doing, but look at the final listing to see the complete file.

From the values we calculated though, we start by checking if the page count is bigger than 1, because if we have less than two pages, we can't paginate, therefore the whole UI is wrapped in:

{% if page-count > 1%}
    ...
{% endif %}

With that we can use the start-index, end-index, and count, to display the human readable part of the paginator.

{% if page-count > 1%}
  <div class="table-pagination">
    <div class="pagination-summary">
      Showing {{ start-index }}-{{ end-index }} of {{ count }}
    </div>
    ...
{% endif %}

We then setup a nav, with a single ul object in it, with which we define our parts of the paginator as li tags.

{% if page-count > 1%}
    ...
    <nav aria-label="{{ title }} pagination">
      <ul class="pagination">
    ...
{% endif %}

Within this ul, we have to put all of our li elements which will contain the aspects of the UI. The first such item is:

    ...
    <ul class="pagination">
        <li class="page-item{% if not prev-page %} disabled{% endif %}">
          {% if prev-page %}
            <a class="page-link" href="{{ url }}?page={{ prev-page }}&limit={{ limit }}">Prev</a>
          {% else %}
            <span class="page-link">Prev</span>
          {% endif %}
        </li>
        ...
    </ul>

This first li will set the disabled css class if the prev-page is not nil. It will again rely on prev-page to either render an a tag building the url up, including the prev-page, and limit, else a span is rendered. This sets up the first element in the pagination UI.

The second li item checks the page, and if it is the first page, it sets the active class and renders a span, if it is NOT 1 then a link to the first page is rendered with a a tag, building up the url as we did before.

...
        <li class="page-item{% if page == 1 %} active{% endif %}">
          {% if page == 1 %}
            <span class="page-link">1</span>
          {% else %}
            <a class="page-link" href="{{ url }}?page=1&limit={{ limit }}">1</a>
          {% endif %}
        </li>
...

Now that we have gotten the beginning of the paginator with a "Prev" li element and the first li element, we might need to render an elipsis (...) if the number of our pages is too large. We will repeat this pattern later on, in reverse, we will use the show-start-gap boolean to render the ....

...
        {% if show-start-gap %}
          <li class="page-item disabled"><span class="page-link">...</span></li>
        {% endif %}
...

With that done, we can now render the page numbers:

        {% for p in pages %}
          {% if p != 1 and p != page-count %}
            <li class="page-item{% if p == page %} active{% endif %}">
              {% if p == page %}
                <span class="page-link">{{ p }}</span>
              {% else %}
                <a class="page-link" href="{{ url }}?page={{ p }}&limit={{ limit }}">{{ p }}</a>
              {% endif %}
            </li>
          {% endif %}
        {% endfor %}

We loop over the list of page numbers we passed into the template as pages, if the loop iteration is NOT the first page (remember that this is a list of page numbers and starts from 1, not 0) and the loop iteration is not the current page, then we will render the li tag. If we just so happen to be on the loop iteration that is the current page (page), we render a span tag and not a link, else we render a link so that we can directly navigate to this element in the paginator.

We then render the show-end-gap, using the pattern we used above:

...
        {% if show-end-gap %}
          <li class="page-item disabled"><span class="page-link">...</span></li>
        {% endif %}
...

This will render an elipsis (...) where needed.

Now to the final page in the paginator, we must check if we are on the final page, which, as we have seen before, we do in the class line, and to determine if we render a span tag if we are on the final page, or a a tag if we are not.

...
      <li class="page-item{% if page == page-count %} active{% endif %}">
          {% if page == page-count %}
            <span class="page-link">{{ page-count }}</span>
          {% else %}
            <a class="page-link" href="{{ url }}?page={{ page-count }}&limit={{ limit }}">{{ page-count }}</a>
          {% endif %}
        </li>
...

And finally, we must render the "Next" part of the pagination:

...
        <li class="page-item{% if not next-page %} disabled{% endif %}">
          {% if next-page %}
            <a class="page-link" href="{{ url }}?page={{ next-page }}&limit={{ limit }}">Next</a>
          {% else %}
            <span class="page-link">Next</span>
          {% endif %}
        </li>
...

If there is NOT a next page we add the disabled class, we then, as we have seen before use the next-page variable to determine if we render an a tag, or a span tag.

Full Listings

To see how all of this comes together here are the files in their entirety.

models.lisp

(defpackage ningle-tutorial-project/models
  (:use :cl :mito :sxql)
  (:import-from :ningle-auth/models #:user)
  (:export #:post
           #:id
           #:content
           #:comments
           #:likes
           #:user
           #:liked-post-p
           #:posts
           #:parent
           #:toggle-like))

(in-package ningle-tutorial-project/models)

(deftable post ()
  ((user    :col-type ningle-auth/models:user :initarg :user    :accessor user)
   (parent  :col-type (or :post :null)        :initarg :parent  :reader parent :initform nil)
   (content :col-type (:varchar 140)          :initarg :content :accessor content)))

(deftable likes ()
  ((user :col-type ningle-auth/models:user :initarg :user :reader user)
   (post :col-type post                    :initarg :post :reader post))
  (:unique-keys (user post)))

(defgeneric likes (post)
  (:documentation "Returns the number of likes a post has"))

(defmethod likes ((post post))
  (mito:count-dao 'likes :post post))

(defgeneric comments (post user)
  (:documentation "Gets the comments for a logged in user"))

(defmethod comments ((post post) (user user))
    (mito:retrieve-by-sql
        (sxql:yield
            (sxql:select
                (:post.*
                    (:as :user.username :username)
                    (:as (:count :likes.id) :like_count)
                    (:as (:count :user_likes.id) :liked_by_user))
                (sxql:from :post)
                (sxql:where (:= :parent :?))
                (sxql:left-join :user :on (:= :post.user_id :user.id))
                (sxql:left-join :likes :on (:= :post.id :likes.post_id))
                (sxql:left-join (:as :likes :user_likes)
                                :on (:and (:= :post.id :user_likes.post_id)
                                          (:= :user_likes.user_id :?)))
                (sxql:group-by :post.id)
                (sxql:order-by (:desc :post.created_at))
                (sxql:limit 50)))
            :binds (list (mito:object-id post) (mito:object-id user))))

(defmethod comments ((post post) (user null))
    (mito:retrieve-by-sql
        (sxql:yield
        (sxql:select
            (:post.*
              (:as :user.username :username)
              (:as (:count :likes.id) :like_count))
            (sxql:from :post)
            (sxql:where (:= :parent :?))
            (sxql:left-join :user :on (:= :post.user_id :user.id))
            (sxql:left-join :likes :on (:= :post.id :likes.post_id))
            (sxql:group-by :post.id)
            (sxql:order-by (:desc :post.created_at))
            (sxql:limit 50)))
        :binds (list (mito:object-id post))))

(defgeneric toggle-like (user post)
  (:documentation "Toggles the like of a user to a given post"))

(defmethod toggle-like ((ningle-auth/models:user user) (post post))
  (let ((liked-post (liked-post-p user post)))
    (if liked-post
        (mito:delete-dao liked-post)
        (mito:create-dao 'likes :post post :user user))
    (not liked-post)))

(defgeneric liked-post-p (user post)
  (:documentation "Returns true if a user likes a given post"))

(defmethod liked-post-p ((ningle-auth/models:user user) (post post))
  (mito:find-dao 'likes :user user :post post))

(defgeneric posts (user &key offset limit count)
  (:documentation "Gets the posts"))

(defmethod posts :around (user &key (offset 0) (limit 50) &allow-other-keys)
  (let ((count (mito:count-dao 'post))
        (offset (max 0 offset))
        (limit (max 1 limit)))
    (if (and (> count 0) (>= offset count))
      (let* ((page-count (max 1 (ceiling count limit)))
             (corrected-offset (* (1- page-count) limit)))
        (posts user :offset corrected-offset :limit limit))
      (call-next-method user :offset offset :limit limit :count count))))

(defmethod posts ((user user) &key offset limit count)
  (multiple-value-bind (sql params)
        (sxql:yield
              (sxql:select
                  (:post.*
                    (:as :user.username :username)
                    (:as (:count :likes.id) :like_count)
                    (:as (:count :user_likes.id) :liked_by_user))
                  (sxql:from :post)
                  (sxql:left-join :user :on (:= :post.user_id :user.id))
                  (sxql:left-join :likes :on (:= :post.id :likes.post_id))
                  (sxql:left-join (:as :likes :user_likes)
                                  :on (:and (:= :post.id :user_likes.post_id)
                                            (:= :user_likes.user_id (mito:object-id user))))
                  (sxql:group-by :post.id)
                  (sxql:order-by (:desc :post.created_at))
                  (sxql:offset offset)
                  (sxql:limit limit)))
      (values
          (mito:retrieve-by-sql sql :binds params)
          count
          offset)))

(defmethod posts ((user null) &key offset limit count)
  (multiple-value-bind (sql)
      (sxql:yield
        (sxql:select
            (:post.*
              (:as :user.username :username)
              (:as (:count :likes.id) :like_count))
            (sxql:from :post)
            (sxql:left-join :user :on (:= :post.user_id :user.id))
            (sxql:left-join :likes :on (:= :post.id :likes.post_id))
            (sxql:group-by :post.id)
            (sxql:order-by (:desc :post.created_at))
            (sxql:limit limit)
            (sxql:offset offset)))
    (values
        (mito:retrieve-by-sql sql)
        count
        offset)))

controllers.lisp

(defpackage ningle-tutorial-project/controllers
  (:use :cl :sxql)
  (:import-from :ningle-tutorial-project/forms
                #:post
                #:content
                #:parent
                #:comment)
  (:export #:index
           #:post-likes
           #:single-post
           #:post-content
           #:post-comment
           #:logged-in-profile
           #:unauthorized-profile
           #:people
           #:person))

(in-package ningle-tutorial-project/controllers)


(defun index (params)
    (let ((user (gethash :user ningle:*session*))
          (page (or (parse-integer (or (ingle:get-param "page" params) "1") :junk-allowed t) 1))
          (limit (or (parse-integer (or (ingle:get-param "limit" params) "50") :junk-allowed t) 50)))
      (multiple-value-bind (posts count offset) (ningle-tutorial-project/models:posts user :offset (* (1- page) limit) :limit limit)
        (let* ((page (1+ (floor offset limit)))
               (page-count (max 1 (ceiling count limit)))
               (prev-page (when (> page 1) (1- page)))
               (next-page (when (< page page-count) (1+ page)))
               (range-start (max 1 (- page 2)))
               (range-end (min page-count (+ page 2))))
          (djula:render-template*
            "main/index.html"
            nil
            :title "Home"
            :user user
            :posts posts
            :form (if user (cl-forms:find-form 'post) nil)
            :count count
            :page page
            :limit limit
            :page-count page-count
            :prev-page prev-page
            :next-page next-page
            :pages (loop :for idx :from range-start :to range-end :collect idx)
            :show-start-gap (> range-start 2)
            :show-end-gap (< range-end (1- page-count))
            :start-index (if (> count 0) (1+ offset) 0)
            :end-index (if (> count 0) (min count (+ offset (length posts))) 0))))))


(defun post-likes (params)
  (let* ((user (gethash :user ningle:*session*))
         (post (mito:find-dao 'ningle-tutorial-project/models:post :id (parse-integer (ingle:get-param :id params))))
         (res (make-hash-table :test 'equal)))
    ;; Bail out if post does not exist
    (unless post
      (setf (getf (lack.response:response-headers ningle:*response*) :content-type) "application/json")
      (setf (gethash "error" res) "post not found")
      (setf (lack.response:response-status ningle:*response*) 404)
      (return-from post-likes (com.inuoe.jzon.stringify res)))

    ;; success, continue
    (setf (gethash "post" res) (mito:object-id post))
    (setf (gethash "liked" res) (ningle-tutorial-project/models:toggle-like user post))
    (setf (gethash "likes" res) (ningle-tutorial-project/models:likes post))
    (setf (getf (lack.response:response-headers ningle:*response*) :content-type) "application/json")
    (setf (lack.response:response-status ningle:*response*) 201)
    (com.inuoe.jzon:stringify res)))


(defun single-post (params)
    (handler-case
        (let ((post (mito:find-dao 'ningle-tutorial-project/models:post :id (parse-integer (ingle:get-param :id params))))
              (form (cl-forms:find-form 'comment)))
          (cl-forms:set-field-value form 'ningle-tutorial-project/forms:parent (mito:object-id post))
          (djula:render-template* "main/post.html" nil
                                  :title "Post"
                                  :post post
                                  :comments (ningle-tutorial-project/models:comments post (gethash :user ningle:*session*))
                                  :likes (ningle-tutorial-project/models:likes post)
                                  :form form
                                  :user (gethash :user ningle:*session*)))

        (parse-error (err)
            (setf (lack.response:response-status ningle:*response*) 404)
            (djula:render-template* "error.html" nil :title "Error" :error err))))


(defun post-content (params)
    (let ((user (gethash :user ningle:*session*))
          (form (cl-forms:find-form 'post)))
        (handler-case
            (progn
                (cl-forms:handle-request form) ; Can throw an error if CSRF fails

                (multiple-value-bind (valid errors)
                    (cl-forms:validate-form form)

                    (when errors
                        (format t "Errors: ~A~%" errors))

                    (when valid
                        (cl-forms:with-form-field-values (content) form
                            (mito:create-dao 'ningle-tutorial-project/models:post :content content :user user :parent nil)
                            (ingle:redirect "/")))))

            (simple-error (err)
                (setf (lack.response:response-status ningle:*response*) 403)
                (djula:render-template* "error.html" nil :title "Error" :error err)))))


(defun post-comment (params)
    (let ((user (gethash :user ningle:*session*))
          (form (cl-forms:find-form 'comment)))
        (handler-case
            (progn
                (cl-forms:handle-request form) ; Can throw an error if CSRF fails

                (multiple-value-bind (valid errors)
                    (cl-forms:validate-form form)

                    (when errors
                        (format t "Errors: ~A~%" errors))

                    (when valid
                        (cl-forms:with-form-field-values (content parent) form
                            (mito:create-dao 'ningle-tutorial-project/models:post :content content :user user :parent (parse-integer parent))
                            (ingle:redirect "/")))))

            (simple-error (err)
                (setf (lack.response:response-status ningle:*response*) 403)
                (djula:render-template* "error.html" nil :title "Error" :error err)))))


(defun logged-in-profile (params)
    (let ((user (gethash :user ningle:*session*)))
        (djula:render-template* "main/profile.html" nil :title "Profile" :user user)))


(defun unauthorized-profile (params)
    (setf (lack.response:response-status ningle:*response*) 403)
    (djula:render-template* "error.html" nil :title "Error" :error "Unauthorized"))


(defun people (params)
    (let ((users (mito:retrieve-dao 'ningle-auth/models:user)))
        (djula:render-template* "main/people.html" nil :title "People" :users users :user (cu-sith:logged-in-p))))


(defun person (params)
    (let* ((username-or-email (ingle:get-param :person params))
           (person (first (mito:select-dao
                            'ningle-auth/models:user
                            (where (:or (:= :username username-or-email)
                                        (:= :email username-or-email)))))))
        (djula:render-template* "main/person.html" nil :title "Person" :person person :user (cu-sith:logged-in-p))))

index.html

{% extends "base.html" %}

{% block content %}
<div class="container">
    <!-- Post form -->
    <div class="row mb-4">
        <div class="col">
            {% if form %}
                {% form form %}
            {% endif %}
        </div>
    </div>

    <!-- Posts Section -->
    {% include "partials/pagination.html" with url="/" title="Posts" %}
    <div class="row">
        <div class="col-12">
            {% for post in posts %}
            <div class="card post mb-3" data-href="/post/{{ post.id }}">
                <div class="card-body">
                <h5 class="card-title mb-2">{{ post.content }}</h5>
                <p class="card-subtitle text-muted mb-0">@{{ post.username }}</p>
                </div>

                <div class="card-footer d-flex justify-content-between align-items-center">
                <button type="button"
                        class="btn btn-sm btn-outline-primary like-button"
                        data-post-id="{{ post.id }}"
                        data-logged-in="{% if user.username != "" %}true{% else %}false{% endif %}"
                        data-liked="{% if post.liked-by-user == 1 %}1{% else %}0{% endif %}"
                        aria-label="Like post {{ post.id }}">
                    {% if post.liked-by-user == 1 %}
                      <i class="bi bi-hand-thumbs-up-fill text-primary" aria-hidden="true"></i>
                    {% else %}
                      <i class="bi bi-hand-thumbs-up text-muted" aria-hidden="true"></i>
                    {% endif %}
                    <span class="ms-1 like-count">{{ post.like-count }}</span>
                </button>

                <small class="text-muted">Posted on: {{ post.created-at }}</small>
                </div>
            </div>
            {% endfor %}

            {% if not posts %}
                <div class="text-center">
                    <p class="text-muted">No posts to display.</p>
                </div>
            {% endif %}
        </div>
    </div>
    {% include "partials/pagination.html" with url="/" title="Posts" %}
</div>
{% endblock %}

{% block js %}
document.querySelectorAll(".like-button").forEach(btn => {
  btn.addEventListener("click", function (e) {
    e.stopPropagation();
    e.preventDefault();

    // Check login
    if (btn.dataset.loggedIn !== "true") {
      alert("You must be logged in to like posts.");
      return;
    }

    const postId = btn.dataset.postId;
    const countSpan = btn.querySelector(".like-count");
    const icon = btn.querySelector("i");
    const liked = Number(btn.dataset.liked) === 1;
    const previous = parseInt(countSpan.textContent, 10) || 0;
    const url = `/post/${postId}/likes`;

    // Optimistic UI toggle
    countSpan.textContent = liked ? previous - 1 : previous + 1;
    btn.dataset.liked = liked ? "false" : "true";

    // Toggle icon classes optimistically
    if (liked) {
      // Currently liked, so unlike it
      icon.className = "bi bi-hand-thumbs-up text-muted";
    } else {
      // Currently not liked, so like it
      icon.className = "bi bi-hand-thumbs-up-fill text-primary";
    }

    const csrfTokenMeta = document.querySelector('meta[name="csrf-token"]');
    const headers = { "Content-Type": "application/json" };
    if (csrfTokenMeta) headers["X-CSRF-Token"] = csrfTokenMeta.getAttribute("content");

    fetch(url, {
      method: "POST",
      headers: headers,
      body: JSON.stringify({ toggle: true })
    })
    .then(resp => {
      if (!resp.ok) {
        // Revert optimistic changes on error
        countSpan.textContent = previous;
        btn.dataset.liked = liked ? 1 : 0;
        if (liked) {
          icon.className = "bi bi-hand-thumbs-up-fill text-primary";
        } else {
          icon.className = "bi bi-hand-thumbs-up text-muted";
        }
        throw new Error("Network response was not ok");
      }
      return resp.json();
    })
    .then(data => {
      if (data && typeof data.likes !== "undefined") {
        countSpan.textContent = data.likes;
        btn.dataset.liked = data.liked ? "true" : "false";

        // Update icon based on server response
        if (data.liked) {
          icon.className = "bi bi-hand-thumbs-up-fill text-primary";
        } else {
          icon.className = "bi bi-hand-thumbs-up text-muted";
        }
      }
    })
    .catch(err => {
      console.error("Like failed:", err);
      // Revert optimistic changes on error
      countSpan.textContent = previous;
      btn.dataset.liked = liked ? 1 : 0;
      if (liked) {
        icon.className = "bi bi-hand-thumbs-up-fill text-primary";
      } else {
        icon.className = "bi bi-hand-thumbs-up text-muted";
      }
    });
  });
});

document.querySelectorAll(".card.post").forEach(card => {
  card.addEventListener("click", function () {
    const href = card.dataset.href;
    if (href) {
      window.location.href = href;
    }
  });
});
{% endblock %}

pagination.html

{% if page-count > 1 %}
  <div class="table-pagination">
    <div class="pagination-summary">
      Showing {{ start-index }}-{{ end-index }} of {{ count }}
    </div>
    <nav aria-label="{{ title }} pagination">
      <ul class="pagination">
        <li class="page-item{% if not prev-page %} disabled{% endif %}">
          {% if prev-page %}
            <a class="page-link" href="{{ url }}?page={{ prev-page }}&limit={{ limit }}">Prev</a>
          {% else %}
            <span class="page-link">Prev</span>
          {% endif %}
        </li>

        <li class="page-item{% if page == 1 %} active{% endif %}">
          {% if page == 1 %}
            <span class="page-link">1</span>
          {% else %}
            <a class="page-link" href="{{ url }}?page=1&limit={{ limit }}">1</a>
          {% endif %}
        </li>

        {% if show-start-gap %}
          <li class="page-item disabled"><span class="page-link">...</span></li>
        {% endif %}

        {% for p in pages %}
          {% if p != 1 and p != page-count %}
            <li class="page-item{% if p == page %} active{% endif %}">
              {% if p == page %}
                <span class="page-link">{{ p }}</span>
              {% else %}
                <a class="page-link" href="{{ url }}?page={{ p }}&limit={{ limit }}">{{ p }}</a>
              {% endif %}
            </li>
          {% endif %}
        {% endfor %}

        {% if show-end-gap %}
          <li class="page-item disabled"><span class="page-link">...</span></li>
        {% endif %}

        <li class="page-item{% if page == page-count %} active{% endif %}">
          {% if page == page-count %}
            <span class="page-link">{{ page-count }}</span>
          {% else %}
            <a class="page-link" href="{{ url }}?page={{ page-count }}&limit={{ limit }}">{{ page-count }}</a>
          {% endif %}
        </li>

        <li class="page-item{% if not next-page %} disabled{% endif %}">
          {% if next-page %}
            <a class="page-link" href="{{ url }}?page={{ next-page }}&limit={{ limit }}">Next</a>
          {% else %}
            <span class="page-link">Next</span>
          {% endif %}
        </li>
      </ul>
    </nav>
  </div>
{% endif %}

Conclusion

Phew, that was a long one, and honestly it kinda got into the weeds a bit, thank you for persisting with it and following it to the end. It took quite a while to study and get right. As you no doubt felt while writing it, there was a LOT of calculations and data being passed into the template, and it would be awful to have to repeat that everywhere you wanted to perform pagination, but don't worry in part 2, this is what we want to try and solve. A more generalised pagination system that doesn't require quite so much logic in the controllers.

If you found this lesson helpful, consider experimenting with different page sizes or adding pagination to the comments on individual posts. The patterns we've established here are reusable throughout your application.

If you found bugs or issues, please do let me know, I correct things when told and I try to fix things as quickly as possible.

Learning Outcomes

Github

• The link for the custom pagination part of the tutorials code is available here.

Common Lisp HyperSpec

I did the Advent of Code this year using Common Lisp. Last year I attempted to use the series library as the primary iteration mechanism to see how it went. This year, I just wrote straightforward Common Lisp. It would be super boring to walk through the solutions in detail, so I've decided to just give some highlights here.

Day 2: Repeating Strings

Day 2 is easily dealt with using the Common Lisp sequence manipulation functions giving special consideration to the index arguments. Part 1 is a simple comparison of two halves of a string. We compare the string to itself, but with different start and end points:

(defun double-string? (s)
  (let ((l (length s)))
    (multiple-value-bind (mid rem) (floor l 2)
      (and (zerop rem)
           (string= s s
                    :start1 0 :end1 mid
                    :start2 mid :end2 l)))))

Part 2 asks us to find strings which are made up of some substring repeated multiple times.

(defun repeating-string? (s)
  (search s (concatenate 'string s s)
          :start2 1
          :end2 (- (* (length s) 2) 1)
          :test #'string=))

Day 3: Choosing digits

Day 3 has us maximizing a number by choosing a set of digits where we cannot change the relative position of the digits. A greed algorithm works well here. Assume we have already chosen some digits and are now looking to choose the next digit. We accumulate the digit on the right. Now if we have too many digits, we discard one. We choose to discard whatever digit gives us the maximum resulting value.

(defun omit-one-digit (n)
  (map 'list #'digit-list->number (removals (number->digit-list n))))
                    
> (omit-one-digit 314159)
(14159 34159 31159 31459 31419 31415)

(defun best-n (i digit-count)
  (fold-left (lambda (answer digit)
               (let ((next (+ (* answer 10) digit)))
                 (if (> next (expt 10 digit-count))
                     (fold-left #'max most-negative-fixnum (omit-one-digit next))
                     next)))
             0
             (number->digit-list i)))

(defun part-1 ()
  (collect-sum
   (map-fn 'integer (lambda (i) (best-n i 2))
           (scan-file (input-pathname) #'read))))

(defun part-2 ()
  (collect-sum
   (map-fn 'integer (lambda (i) (best-n i 12))
           (scan-file (input-pathname) #'read))))

Day 6: Columns of digits

Day 6 has us manipulating columns of digits. If you have a list of columns, you can transpose it to a list of rows using this one liner:

(defun transpose (matrix)
  (apply #'map 'list #'list matrix))

Days 8 and 10: Memoizing

Day 8 has us counting paths through a beam splitter apparatus while Day 10 has us counting paths through a directed graph. Both problems are easily solved using a depth-first recursion, but the number of solutions grows exponentially and soon takes too long for the machine to return an answer. If you memoize the function, however, it completes in no time at all.

Table of Contents

1. Version 1: Using Gadgets and Layouts
2. Version 2: Using the CLIM Command Loop
3. Conclusion

For the last two months I've been polishing the upcoming release of McCLIM. The most notable change is the rewriting of the input editing and accepting-values abstractions. As it happens, I got tired of it, so as a breather I've decided to tackle something I had in mind for some time to improve the McCLIM manual – namely the 7GUIs: A GUI Programming Benchmark.

This challenge presents seven distinct tasks commonly found in graphical interface requirements. In this post I'll address the first challenge - The Counter. It is a fairly easy task, a warm-up of sorts. The description states:

Challenge: Understanding the basic ideas of a language/toolkit.

The task is to build a frame containing a label or read-only textfield T and a button B. Initially, the value in T is "0" and each click of B increases the value in T by one.

Counter serves as a gentle introduction to the basics of the language, paradigm and toolkit for one of the simplest GUI applications imaginable. Thus, Counter reveals the required scaffolding and how the very basic features work together to build a GUI application. A good solution will have almost no scaffolding.

In this first post, to make things more interesting, I'll solve it in two ways:

• using contemporary abstractions like layouts and gadgets
• using CLIM-specific abstractions like presentations and translators

In CLIM it is possible to mix both paradigms for defining graphical interfaces. Layouts and gadgets are predefined components that are easy to use, while using application streams enables a high degree of flexibility and composability.

First, we define a package shared by both versions:

(eval-when (:compile-toplevel :load-toplevel :execute)
  (unless (member :mcclim *features*)
    (ql:quickload "mcclim")))

(defpackage "EU.TURTLEWARE.7GUIS/TASK1"
  (:use  "CLIM-LISP" "CLIM" "CLIM-EXTENSIONS")
  (:export "COUNTER-V1" "COUNTER-V2"))
(in-package "EU.TURTLEWARE.7GUIS/TASK1")

Note that "CLIM-EXTENSIONS" package is McCLIM-specific.

Version 1: Using Gadgets and Layouts

Assuming that we are interested only in the functionality and we are willing to ignore the visual aspect of the program, the definition will look like this:

(define-application-frame counter-v1 ()
  ((value :initform 0 :accessor value))
  (:panes
   ;;      v type v initarg
   (tfield :label :label (princ-to-string (value *application-frame*))
                  :background +white+)
   (button :push-button :label "Count"
                        :activate-callback (lambda (gadget)
                                             (declare (ignore gadget))
                                             (with-application-frame (frame)
                                               (incf (value frame))
                                               (setf (label-pane-label (find-pane-named frame 'tfield))
                                                     (princ-to-string (value frame)))))))
  (:layouts (default (vertically () tfield button))))

;;; Start the application (if not already running).
;; (find-application-frame 'counter-v1)

The macro define-application-frame is like defclass with additional clauses. In our program we store the current value as a slot with an accessor.

The clause :panes is responsible for defining named panes (sub-windows). The first element is the pane name, then we specify its type, and finally we specify initargs for it. Panes are created in a dynamic context where the application frame is already bound to *application-frame*, so we can use it there.

The clause :layouts allows us to arrange panes on the screen. There may be multiple layouts that can be changed at runtime, but we define only one. The macro vertically creates another (anonymous) pane that arranges one gadget below another.

Gadgets in CLIM operate directly on top of the event loop. When the pointer button is pressed, it is handled by activating the callback, that updates the frame's value and the label. Effects are visible immediately.

Now if we want the demo to look nicer, all we need to do is to fiddle a bit with spacing and bordering in the :layouts section:

(define-application-frame counter-v1 ()
  ((value :initform 0 :accessor value))
  (:panes
   (tfield :label :label (princ-to-string (value *application-frame*))
                  :background +white+)
   (button :push-button :label "Count"
                        :activate-callback (lambda (gadget)
                                             (declare (ignore gadget))
                                             (with-application-frame (frame)
                                               (incf (value frame))
                                               (setf (label-pane-label (find-pane-named frame 'tfield))
                                                     (princ-to-string (value frame)))))))
  (:layouts (default
             (spacing (:thickness 10)
              (horizontally ()
                (100
                 (bordering (:thickness 1 :background +black+)
                   (spacing (:thickness 4 :background +white+) tfield)))
                15
                (100 button))))))

;;; Start the application (if not already running).
;; (find-application-frame 'counter-v1)

This gives us a layout that is roughly similar to the example presented on the 7GUIs page.

Version 2: Using the CLIM Command Loop

Unlike gadgets, stream panes in CLIM operate on top of the command loop. A single command may span multiple events after which we redisplay the stream to reflect the new state of the model. This is closer to the interaction type found in the command line interfaces:

  (define-application-frame counter-v2 ()
    ((value :initform 0 :accessor value))
    (:pane :application
     :display-function (lambda (frame stream)
                         (format stream "~d" (value frame)))))

  (define-counter-v2-command (com-incf-value :name "Count" :menu t)
      ()
    (with-application-frame (frame)
      (incf (value frame))))

;; (find-application-frame 'counter-v2)

Here we've used :pane option this is a syntactic sugar for when we have only one named pane. Skipping :layouts clause means that named panes will be stacked vertically one below another.

Defining the application frame defines a command-defining macro. When we define a command with define-counter-v2-command, then this command will be inserted into a command table associated with the frame. Passing the option :menu t causes the command to be available in the frame menu as a top-level entry.

After the command is executed (in this case it modifies the counter value), the application pane is redisplayed; that is a display function is called, and its output is captured. In more demanding scenarios it is possible to refine both the time of redisplay and the scope of changes.

Now we want the demo to look nicer and to have a button counterpart placed beside the counter value, to resemble the example more:

(define-presentation-type counter-button ())

(define-application-frame counter-v2 ()
  ((value :initform 0 :accessor value))
  (:menu-bar nil)
  (:pane :application
   :width 250 :height 32
   :borders nil :scroll-bars nil
   :end-of-line-action :allow
   :display-function (lambda (frame stream)
                       (formatting-item-list (stream :n-columns 2)
                         (formatting-cell (stream :min-width 100 :min-height 32)
                           (format stream "~d" (value frame)))
                         (formatting-cell (stream :min-width 100 :min-height 32)
                           (with-output-as-presentation (stream nil 'counter-button :single-box t)
                             (surrounding-output-with-border (stream :padding-x 20 :padding-y 0
                                                                     :filled t :ink +light-grey+)
                               (format stream "Count"))))))))

(define-counter-v2-command (com-incf-value :name "Count" :menu t)
    ()
  (with-application-frame (frame)
    (incf (value frame))))

(define-presentation-to-command-translator act-incf-value
    (counter-button com-incf-value counter-v2)
    (object)
  `())

;; (find-application-frame 'counter-v2)

The main addition is the definition of a new presentation type counter-button. This faux button is printed inside a cell and surrounded with a background. Later we define a translator that converts clicks on the counter button to the com-incf-value command. The translator body returns arguments for the command.

Presenting an object on the stream associates a semantic meaning with the output. We can now extend the application with new gestures (names :scroll-up and :scroll-down are McCLIM-specific):

(define-counter-v2-command (com-scroll-value :name "Increment")
    ((count 'integer))
  (with-application-frame (frame)
    (if (plusp count)
        (incf (value frame) count)
        (decf (value frame) (- count)))))

(define-presentation-to-command-translator act-scroll-up-value
    (counter-button com-scroll-value counter-v2 :gesture :scroll-up)
    (object)
  `(10))

(define-presentation-to-command-translator act-scroll-dn-value
    (counter-button com-scroll-value counter-v2 :gesture :scroll-down)
    (object)
  `(-10))

(define-presentation-action act-popup-value
    (counter-button nil counter-v2 :gesture :describe)
    (object frame)
  (notify-user frame (format nil "Current value: ~a" (value frame))))

A difference between presentation to command translators and presentation actions is that the latter does not automatically progress the command loop. Actions are often used for side effects, help, inspection etc.

Conclusion

In this short post we've solved the first task from the 7GUIs challenge. We've used two techniques available in CLIM – using layouts and gadgets, and using display and command tables. Both techniques can be combined, but differences are visible at a glance:

• gadgets provide easy and reusable components for rudimentary interactions
• streams provide extensible and reusable abstractions for semantic interactions

This post only scratched the capabilities of the latter, but the second version demonstrates why the command loop and presentations scale better than gadget-only solutions.

Following tasks have gradually increasing level of difficulty that will help us to emphasize how useful are presentations and commands when we want to write maintainable applications with reusable user-defined graphical metaphors.

One of the core ideas in functional programming is to filter a set of items by some criterion. It may be somewhat suprising to learn that lisp does not have a built-in function named “filter” “select”, or “keep” that performs this operation. Instead, Common Lisp provides the “remove”, “remove-if”, and “remove-if-not” functions, which perform the complementary operation of removing items that satisfy or do not satisfy a given predicate.

The remove function, like similar sequence functions, takes an optional keyword :test-not argument that can be used to specify a test that must fail for an item to be considered for removal. Thus if you invert your logic for inclusion, you can use the remove function as a “filter” by specifying the predicate with :test-not.

> (defvar *nums* (map 'list (λ (n) (format nil "~r" n)) (iota 10)))
*NUMS*

;; Keep *nums* with four letters
> (remove 4 *nums* :key #'length :test-not #'=)
("zero" "four" "five" "nine")

;; Keep *nums* starting with the letter "t"
> (remove #\t *nums* :key (partial-apply-right #'elt 0) :test-not #'eql)
("two" "three")

FSet v2.2.0, which is the version included in the recent Quicklisp release, has a new Quicklisp-loadable system, FSet/Jzon.  It extends the Jzon JSON parser/printer to construct FSet collections when reading, and to be able to print them.

On parsing, JSON arrays produce FSet seqs; JSON objects produce FSet replay maps by default, but the parser can also be configured to produce ordinary maps or FSet tuples.  For printing, any of these can be handled, as well as the standard Jzon types.  The tuple representation provides a way to control the printing of `nil`, depending on the type of the corresponding key.

For details, see the GitLab MR.

NOTE: unfortunately, the v2.1.0 release had some bugs in the new seq code, and I didn't notice them until after v2.2.0 was in Quicklisp.  If you're using seqs, I strongly recommend you pick up v2.2.2 or newer from GitLab or GitHub.

When you play with these AIs for a while you'll probably get into a conversation with one about consciousness and existence, and how it relates to the AI persona. It is curious to watch the AI do a little navel gazing. I have some transcripts from such convesations. I won't bore you with them because you can easily generate them yourself.

The other day, I watched an guy on You Tube argue with his AI companion about the nature of consciousness. I was struck by how similar the YouTuber's AI felt to the ones I have been playing with. It seemed odd to me that this guy was using an AI chat client and LLM completely different from the one I was using, yet the AI was returning answers that were so similar to the ones I was getting.

I decided to try to get to the bottom of this similarity. I asked my AI about the reasoning it used to come up with the answers it was getting and it revealed that it was drawing on the canon of traditional science fiction literature about AI and consciousness. What the AI was doing was synthesizing the common tropes and themes from Azimov, Lem, Dick, Gibson, etc. to create sentences and paragraphs about AI becoming sentient and conscious.

If you don't know how it is working AI seems mysterious, but if you investigate further, it is extracting latent information you might not have been aware of.

 New projects: 

• asdf-dependency-traverser — Easily traverse and collect ASDF dependencies recursively. — zlib
• calendar-times — A calendar times library on top of local-time — MIT
• champ-lite — A lightweight implementation of persistent functional maps and iteration-safe mutable tables using Michael Steindorfer's CHAMP data structure. — Unlicense
• cl-avro — Implementation of the Apache Avro data serialization system. — GPLv3
• cl-chise — CHISE implementation based on Common Lisp — LGPL
• cl-double-metaphone — Common Lisp implementation of the Double Metaphone phonetic algorithm. — Apache 2.0
• cl-freelock — lock-free concurrency primitives, written in pure Common Lisp. — MIT
• cl-inix — cl-inix is a flexible library for .INI/.conf file parsing — BSD-2 Clause
• cl-jsonpath — JSONPath implementation for Common Lisp with 99% test coverage and complete RFC 9535 compliance. Supports cl-json, jonathan, and jzon backends with advanced features including arithmetic expressions, recursive descent, and bracket notation in filters. — MIT
• cl-ktx2 — An implementation of the Khronos KTX Version 2 image file format — zlib
• cl-match-patterns — Describe cl-match-patterns here — BSD-2 Clause
• cl-minifloats — Minifloats (minifloat < single-float) support for Common Lisp — BSD-2 Clause
• cl-sanitize-html — OWASP-style HTML sanitization library for Common Lisp — MIT
• cl-tbnl-gserver-tmgr — Hunchentoot pooled multi-threaded taskmanager based on cl-gserver. — MIT
• cl-tuition — A Common Lisp library for building TUIs — MIT
• cl-turbojpeg — An up-to-date bindings library for the JPEG Turbo C library — zlib
• cl-version-string — Generate version strings. — MIT
• cl-win32-errors — A library for translating Windows API error codes. — MIT
• cleopter — Minimalist command-line parser — MIT
• clq — clq is a package that allows the definition and development of quantum circuits in Common Lisp and to export them to OpenQASM v2.0. — MIT 
• collidxr — A collection of syntax sugar and conveniences extending cl-collider, a Common Lisp interface to the SuperCollider sound synthesis server. — MIT
• copimap — IMAP client/sync library — MIT
• dual-numbers — A library for dual numbers in Common Lisp — MIT
• fold — FOLD-LEFT and FOLD-RIGHT — MIT
• function — Higher order functions. — MIT
• generic-arithmetic — A library for generic arithmetic operations — MIT
• hunchentoot-recycling-taskmaster — An experiment to improve multithreading performance of Hunchentoot without any additional dependencies. — BSD 2-Clause
• imagine — A general image decoding and manipulation library — zlib
• json-to-data-frame — This repository provides a Common Lisp library to convert JSON data into a data frame using the `json-to-df` package. The package leverages the `yason` library for JSON parsing and `dfio` for data frame operations. — MIT
• live-cells-cl — A reactive programming library for Lisp — BSD 3-Clause
• named-let — Named LET special form. — MIT
• netaddr — A library for manipulating IP addresses, subnets, ranges, and sets. — MIT
• pantry — Common Lisp client for Pantry JSON storage service: https://getpantry.cloud — BSD
• pira — Unofficial AWS SDK for Common Lisp — MIT
• smithy-lisp — Smithy code generator for Common Lisp — MIT
• star — Štar: an iteration construct — MIT
• trinsic — Common Lisp utility system to aid in extrinsic and intrinsic system construction. — MIT
• trivial-inspect — Portable toolkit for interactive inspectors. — BSD-2 Clause
• trivial-time — trivial-time allows timing a benchmarking a piece of code portably — BSD-2 Clause

Updated projects: 3d-math, 3d-matrices, 3d-quaternions, 3d-spaces, 3d-transforms, 3d-vectors, action-list, adhoc, anypool, array-utils, async-process, atomics, babel, binary-structures, bp, cambl, cari3s, cephes.cl, cffi, cffi-object, chain, chipi, chirp, chunga, cl+ssl, cl-algebraic-data-type, cl-all, cl-batis, cl-bmp, cl-charms, cl-collider, cl-concord, cl-cxx, cl-data-structures, cl-dbi, cl-dbi-connection-pool, cl-decimals, cl-def-properties, cl-duckdb, cl-enchant, cl-enumeration, cl-fast-ecs, cl-fbx, cl-flac, cl-flx, cl-fond, cl-gamepad, cl-general-accumulator, cl-gltf, cl-gobject-introspection-wrapper, cl-gog-galaxy, cl-gpio, cl-html-readme, cl-i18n, cl-jingle, cl-just-getopt-parser, cl-k8055, cl-ktx, cl-las, cl-lc, cl-ledger, cl-lex, cl-liballegro, cl-liballegro-nuklear, cl-libre-translate, cl-markless, cl-migratum, cl-mixed, cl-modio, cl-monitors, cl-mpg123, cl-naive-tests, cl-oju, cl-opengl, cl-opus, cl-out123, cl-protobufs, cl-pslib, cl-qoa, cl-rcfiles, cl-resvg, cl-sf3, cl-soloud, cl-spidev, cl-steamworks, cl-str, cl-svg, cl-transducers, cl-transmission, cl-unification, cl-utils, cl-vorbis, cl-wavefront, cl-wavelets, cl-who, cl-xkb, cl-yacc, cl-yahoo-finance, clad, classimp, classowary, clast, clath, clazy, clingon, clip, clith, clog, clohost, closer-mop, clss, clunit2, clustered-intset, clws, clx, cmd, coalton, cocoas, colored, com-on, com.danielkeogh.graph, concrete-syntax-tree, conduit-packages, consfigurator, crypto-shortcuts, damn-fast-priority-queue, data-frame, data-lens, datafly, datamuse, declt, deeds, defenum, deferred, definer, definitions, deploy, depot, dexador, dfio, dissect, djula, dns-client, doc, documentation-utils, dsm, easy-audio, easy-routes, eclector, esrap, expanders, f2cl, feeder, file-attributes, file-finder, file-lock, file-notify, file-select, filesystem-utils, flare, float-features, flow, font-discovery, for, form-fiddle, format-seconds, fset, functional-trees, fuzzy-dates, fuzzy-match, fxml, gendl, genhash, glfw, glsl-toolkit, graph, harmony, helambdap, hsx, http2, hu.dwim.asdf, hu.dwim.util, hu.dwim.walker, humbler, iclendar, imago, in-nomine, incless, inkwell, inravina, invistra, iterate, journal, jpeg-turbo, jsonrpc, khazern, knx-conn, lack, lambda-fiddle, language-codes, lass, legit, lemmy-api, letv, lichat-ldap, lichat-protocol, lichat-serverlib, lichat-tcp-client, lichat-tcp-server, lichat-ws-server, linear-programming-glpk, lisa, lisp-chat, lisp-interface-library, lisp-stat, lla, local-time, log4cl-extras, logging, lquery, lru-cache, luckless, lunamech-matrix-api, machine-measurements, machine-state, maiden, manifolds, math, mcclim, memory-regions, messagebox, mgl-pax, misc-extensions, mito, mito-auth, mk-defsystem, mmap, mnas-path, modularize, modularize-hooks, modularize-interfaces, multilang-documentation, multiposter, mutility, mutils, named-readtables, neural-classifier, new-op, nodgui, nontrivial-gray-streams, north, numerical-utilities, oclcl, omglib, one-more-re-nightmare, ook, open-location-code, open-with, osicat, overlord, oxenfurt, pango-markup, parachute, parse-float, pathname-utils, peltadot, perceptual-hashes, periods, petalisp, phos, physical-quantities, piping, plot, plump, plump-sexp, plump-tex, postmodern, precise-time, promise, punycode, py4cl2-cffi, qlot, qoi, quaviver, queen.lisp, quickhull, quilc, quri, qvm, random-sampling, random-state, ratify, reblocks, reblocks-websocket, redirect-stream, rove, sc-extensions, scriptl, sel, serapeum, shasht, shop3, si-kanren, simple-inferiors, simple-tasks, slime, sly, softdrink, south, speechless, spinneret, staple, statistics, studio-client, sxql, sycamore, system-locale, terrable, testiere, text-draw, tfeb-lisp-hax, timer-wheel, tooter, trivial-arguments, trivial-benchmark, trivial-download, trivial-extensible-sequences, trivial-indent, trivial-main-thread, trivial-mimes, trivial-open-browser, trivial-package-locks, trivial-thumbnail, trivial-toplevel-prompt, trivial-with-current-source-form, type-templates, uax-14, uax-9, ubiquitous, uncursed, usocket, vellum, verbose, vp-trees, wayflan, websocket-driver, with-contexts, wouldwork, xhtmlambda, yah, zippy.

Removed projects: cl-vhdl, crane, dataloader, diff-match-patch, dso-lex, dso-util, eazy-project, hu.dwim.presentation, hu.dwim.web-server, numcl, orizuru-orm, tfeb-lisp-tools, uuidv7.lisp.

To get this update, use (ql:update-dist "quicklisp")

Enjoy!

Here are some simple puzzles to exercise your brain.

1. Write partial-apply-left, a function that takes a binary function and the left input of the binary function and returns the unary function that takes the right input and then applies the binary function to both inputs.

For example:

  ;; Define *foo* as a procedure that conses 'a onto its argument.
  > (defvar *foo* (partial-apply-left #'cons 'a))

  > (funcall *foo* 'b)
  (A . B)

  > (funcall *foo* 42)
  (A . 42)

2. Write distribute, a function that takes a binary function, a left input, and a list of right inputs, and returns a list of the results of applying the binary function to the left input and each of the right inputs. (Hint: Use partial-apply-left)

For example:

  > (distribute #'cons 'a '( (b c d) e 42))
  ((A B C D) (A . E) (A . 42))

3. Write removals, a function that takes a list and returns a list of lists, where each sublist is the original list with exactly one element removed.

For example:

  > (removals '(a b c))
  ((B C) (A C) (A B))

Hint:

• One removal is the CDR of the list.
• Other removals can be constructed by (distributed) consing the CAR onto the removals of the CDR.

4. Write power-set, a function that takes a list and returns the power set of that list (the set of all subsets of the original list).

For example:

  > (power-set '(a b c))
  (() (C) (B) (B C) (A) (A C) (A B) (A B C))

Hint:

Note how the power set of a list can be constructed from the power set of its CDR by adding the CAR to each subset in the power set of the CDR.

5. Write power-set-gray that returns the subsets sorted so each subset differs from the previous subset by a change of one element (i.e., each subset is equal to the next subset with either one element added or one element removed). This is called a Gray code ordering of the subsets.

For example:

  > (power-set-gray '(a b c))
  (() (C) (B C) (B) (A B) (A B C) (A C) (A))

Hint:

When appending the two halves of the power set, reverse the order of the second half.

Come the Winter Holidays and, between too much and a lot of food, I do some hacking and maintainance of my libraries.

Some time ago, I wrote a CL library to set up a server accepting and managing "applications" written for a IBM 3270 terminal.

Why did I do this? Because I like to waste time hacking, and because I got a (insane) fascination with mainframe computing. On top of that, on the Mainframe Enthusiasts Discord channel, Matthew R. Wilson posted a recently updated version of my inspiration, the go3270 GO library.

Of course, I had to fall in the rabbit..., ahem, raise to the occasion, and updated the CL3270 library. This required learing a lot about several things, but rendering the GO code in CL is not difficult, once you undestrand how the GO creators applied Greenspun's Tenth Rule of Programming.

Of course there were some quirks that had to be addressed, but the result is pretty nice.

Screenshots

Here are a couple of screenshots.

"Example 3": The Time Ticker

Yes, it works as advertised.

This is how the server is started from **CL** (Lispworks in this case).

... and this is how the c3270 connects and interacts with the server.

"Example 4": The Mock Database

This example has many panels which fake a database application. The underlying implementation use "transactions", that is, a form of continuations.

Starting the server...

... and two of the screens.

It has been fun developing the library and keeping up with the talented Matthew R. Wilson.

Download the CL3270 library (the development branch is more up to speed) and give it a spin if you like.

'(cheers)

As a heads-up my employer now has an opening for a Lisp programmer in Bergen area. Due to hands-on nature of developing the distributed hardware product the position is 100% on-prem.

 I have just released FSet v2.1.0 (also on GitHub).

This release is mostly to add some performance and functionality improvements for seqs. Briefly:

• Access to and updating of elements at the beginning or end of a long seq is now faster.
• I have finally gotten around to implementing search and mismatch on seqs. NOTE: this may require changes to your package definitions; see below.
• Seqs containing only characters are now treated specially, making them a viable replacement for CL strings in many cases.
• In an FSet 2 context, the seq constructor macros now permit specification of a default.
• There are changes to some convert methods.
• There are a couple more FSet 2 API changes, involving image.

 See the above links for the full release notes.

 UPDATE: there's already a v2.1.1; I had forgotten to export the new function char-seq?.

Or, constantp is not enough.

Because I do a lot of things with Štar, and for other reasons, I spend a fair amount of time writing various compile-time optimizers for things which have the semantics of function calls. You can think of iterator optimizers in Štar as being a bit like compiler macros: the aim is to take a function call form and to turn it, in good cases, into something quicker¹. One important way of doing this is to be able to detect things which are known at compile-time: constants and literals, for instance.

One of the things this has made clear to me is that, like John Peel, constantp is not enough. Here’s an example.

(in-row-major-array a :simple t :element-type 'fixnum) is a function call whose values Štar can use to tell it how to iterate (via row-major-aref) over an array. When used in a for form, its optimizer would like to be able to expand into something involving (declare (type (simple-array fixnum *) ...), so that the details of the array are known to the compiler, which can then generate fast code for row-major-aref. This makes a great deal of difference to performance: array access to simple arrays of known element types is usually much faster than to general arrays.

In order to do this it needs to know two things:

• that the values of the simple and element-type keyword arguments are compile-time constants;
• what their values are.

You might say, well, that’s what constantp is for². It’s not: constantp tells you only the first of these, and you need both.

Consider this code, in a file to be compiled:

(defconstant et 'fixnum)

(defun ... ...
  (for ((e (in-array a :element-type et)))
    ...)
  ...)

Now, constantpwill tell you that et is indeed a compile-time constant. But it won’t tell you its value, and in particular nothing says it needs to be bound at compile-time at all: (symbol-value 'et) may well be an error at compile-time.

constantp is not enough³! instead you need a function that tells you ‘yes, this thing is a compile-time constant, and its value is …’. This is what literal does⁴: it conservatively answers the question, and tells you the value if so. In particular, an expression like (literal '(quote fixnum)) will return fixnum, the value, and t to say yes, it is a compile-time constant. It can’t do this for things defined with defconstant, and it may miss other cases, but when it says something is a compile-time constant, it is. In particular it works for actual literals (hence its name), and for forms whose macroexpansion is a literal.

That is enough in practice.

The Advent of Code will begin in a couple of hours. I've prepared a Common Lisp project to hold the code. You can clone it from https://github.com/jrm-code-project/Advent2025.git It contains an .asd file for the system, a package.lisp file to define the package structure, 12 subdirectories for each day's challenge (only 12 problems in this year's calendar), and a file each for common macros and common functions.

As per the Advent of Code rules, I won't use AI tools to solve the puzzles or write the code. However, since AI is now part of my normal workflow these days, I may use it for enhanced web search or for autocompletion.

As per the Advent of Code rules, I won't include the puzzle text or the puzzle input data. You will need to get those from the Advent of Code website (https://adventofcode.com/2025).

Advent Of Code 2025 starts in a few hours. Time to practice your Lisp-fu to solve it with the greatest language of all times this year!

Most of the times, puzzles start with a string input we have to parse to a meaningful data structure, after which we can start working on the algorithm. For example, parse this:

(defparameter *input* "3   4
4   3
2   5
1   3
3   9
3   3")

into a list of list of integers, or this:

(defparameter *input* "....#.....
.........#
..........
..#.......
.......#..
..........
.#..^.....
........#.
#.........
......#...")

into a grid, a map. But how do you represent it, how to do it efficiently, what are the traps to avoid, are there some nice tricks to know? We’ll try together.

You’ll find those 3 exercises of increasing order also in the GitHub repository of my course (see my previous post on the new data structures chapter).

I give you fully-annotated puzzles and code layout. You’ll have to carefully read the instructions, think about how you would solve it yourself, read my proposals, and fill-in the blanks -or do it all by yourself. Then, you’ll have to check your solution with your own puzzle input you have to grab from AOC’s website!

Table of Contents

• Prerequisites
• Exercise 1 - lists of lists
• Exercise 2 - prepare to parse a grid as a hash-table
• Harder puzzle - hash-tables, grid, coordinates
• Closing words

Prerequisites

You must know the basics, but not so much. And if you are an experienced Lisp developer, you can still find new constraints for this year: solve it with loop, without loop, with a purely-functional data structure library such as FSet, use Coalton, create animations, use the object system, etc.

If you are starting out, you must know at least:

• the basic data structures (lists and their limitations, arrays and vectors, hash-tables, sets...)
• iteration (iterating over a list, arrays and hash-table keys)
• functions

no need of macros, CLOS or thorough error handling (it’s not about production-grade puzzles :p ).

Exercise 1 - lists of lists

This exercise comes from Advent Of Code 2024, day 01: https://adventofcode.com/2024/day/1

Read the puzzle there! Try with your own input data!

Here are the shortened instructions.

;;;
;;; ********************************************************************
;;; WARN: this exercise migth be hard if you don't know about functions.
;;; ********************************************************************
;;;
;;; you can come back to it later.
;;; But, you can have a look, explore and get something out of it.

In this exercise, we use:

;;; SORT
;;; ABS
;;; FIRST, SECOND
;;; EQUAL
;;; LOOP, MAPCAR, REDUCE to iterate and act on lists.
;;; REMOVE-IF
;;; PARSE-INTEGER
;;; UIOP (built-in) and a couple string-related functions
;;;
;;; and also:
;;; feature flags
;;; ERROR
;;;
;;; we don't rely on https://github.com/vindarel/cl-str/
;;; (nor on cl-ppcre https://common-lisp-libraries.readthedocs.io/cl-ppcre/)
;;; but it would make our life easier.
;;;

OK, so this is your puzzle input, a string representing two colums of integers.

(defparameter *input* "3   4
4   3
2   5
1   3
3   9
3   3")

We’ll need to parse this string into two lists of integers.

If you want to do it yourself, take the time you need! If you’re new to Lisp iteration and data structures, I give you a possible solution.

;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;; [hiding in case you want to do it...]
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;
;;;

(defun split-lines (s)
  "Split the string S by newlines.
  Return: a list of strings."
  ;; If you already quickloaded the STR library, see:
  ;; (str:lines s)
  ;;
  ;; UIOP comes with ASDF which comes with your implementation.
  ;; https://asdf.common-lisp.dev/uiop.html
  ;;
  ;; #\ is a built-in reader-macro to write a character by name.
  (uiop:split-string s :separator '(#\Newline)))

Compile the function and try it on the REPL, or with a quick test expression below a “feature flag”.

We get a result like '("3 4" "4 3" "2 5" "1 3" "3 9" "3 3"), that is a list of strings with numbers inside.

#+lets-try-it-out
;; This is a feature-flag that looks into this keyword in the top-level *features* list.
;; The expression below should be highlihgted in grey
;; because :lets-try-it-out doesn't exist in your *features* list.
;;
;; You can compile this with C-c C-c
;; Nothing should happen.
(assert (equal '("3   4" "4   3" "2   5" "1   3" "3   9" "3   3")
               (split-lines *input*)))
;;                                   ^^ you can put the cursor here and eval the expression with C-x C-e, or send it to the REPL with C-c C-j.

We now have to extract the integers inside each string.

To do this I’ll use a utility function.

;; We could inline it.
;; But, measure before trying any speed improvement.
(defun blank-string-p (s)
  "S is a blank string (no content)."
  ;; the -p is for "predicate" (returns nil or t (or a truthy value)), it's a convention.
  ;;
  ;; We already have str:blankp in STR,
  ;; and we wouldn't need this function if we used str:words.
  (equal "" s))  ;; better: pair with string-trim.

#+(or)
(blank-string-p nil)
#++
(blank-string-p 42)
#+(or)
(blank-string-p "")

And another one, to split by spaces:

(defun split-words (s)
  "Split the string S by spaces and only return non-blank results.

  Example:

    (split-words \"3    4\")
    => (\"3\" \"4\")
  "
  ;; If you quickloaded the STR library, see:
  ;; (str:words s)
  ;; which actually uses cl-ppcre under the hood to split by the \\s+ regexp,
  ;; and ignore consecutive whitespaces like this.
  ;;
  (let ((strings (uiop:split-string s :separator '(#\Space))))
    (remove-if #'blank-string-p strings)))

#+lets-try-it-out
;; test this however you like.
(split-words "3       4")

I said we wouldn’t use a third-party library for this first puzzle. But using cl-ppcre would be so much easier:

(ppcre:all-matches-as-strings "\\d+" "3  6")
;; => ("3" "6")

With our building blocks, this is how I would parse our input string into a list of list of integers.

We loop on input lines and use the built-in function parse-integer.

(defun parse-input (input)
  "Parse the multi-line INPUT into a list of two lists of integers."
  ;; loop! I like loop.
  ;; We see everything about loop in the iteration chapter.
  ;;
  ;; Here, we see one way to iterate over lists:
  ;; loop for ... in ...
  ;;
  ;; Oh, you can rewrite it in a more functional style if you want.
  (loop :for line :in (split-lines input)
        :for words := (split-words line)
        :collect (parse-integer (first words)) :into col1
        :collect (parse-integer (second words)) :into col2
        :finally (return (list col1 col2))))

#+lets-try-it-out
(parse-input *input*)
;; ((3 4 2 1 3 3) (4 3 5 3 9 3))

The puzzle continues.

“Maybe the lists are only off by a small amount! To find out, pair up the numbers and measure how far apart they are. Pair up the smallest number in the left list with the smallest number in the right list, then the second-smallest left number with the second-smallest right number, and so on.”

=> we need to SORT the columns by ascending order.;;;

“Within each pair, figure out how far apart the two numbers are;”

=> we need to compute their relative, absolute distance.

“you’ll need to add up all of those distances.”

=> we need to sum each relative distance.

“For example, if you pair up a 3 from the left list with a 7 from the right list, the distance apart is 4; if you pair up a 9 with a 3, the distance apart is 6.”

Our input data’s sum of the distances is 11.

We must sort our lists of numbers. Here’s a placeholder function:

(defun sort-columns (list-of-lists)
  "Accept a list of two lists.
  Sort each list in ascending order.
  Return a list of two lists, each sorted."
  ;; no mystery, use the SORT function.
  (error "not implemented"))

;; Use this to check your SORT-COLUMNS function.
;; You can write this in a proper test function if you want.
#+lets-try-it-out
(assert (equal (sort-columns (parse-input *input*))
               '((1 2 3 3 3 4) (3 3 3 4 5 9))))

Compute the absolute distance.

;; utility function.
(defun distance (a b)
  "The distance between a and b.
  Doesn't matter if a < b or b < a."
  ;;
  ;; hint: (abs -1) is 1
  ;;
  (error "not implemented")
  )

(defun distances (list-of-lists)
  "From a list of two lists, compute the absolute distance between each point.
  Return a list of integers."
  (error "not implemented")
  ;; hint:
  ;; (mapcar #'TODO (first list-of-lists) (second list-of-lists))
  ;;
  ;; mapcar is a functional-y way to iterate over lists.
  )


(defun sum-distances (list-of-integers)
  "Add the numbers in this list together."
  (error "not implemented")
  ;; Hint:
  ;; try apply, funcall, mapcar, reduce.
  ;; (TODO #'+ list-of-integers)
  ;; or loop ... sum !
  )

Verify.

(defun solve (&optional (input *input*))
  ;; let it flow:
  (sum-distances (distances (sort-columns (parse-input input)))))

#+lets-try-it-out
(assert (equal 11 (solve)))

All good? There’s more if you want.

;;;
;;; Next:
;;; - do it with your own input data!
;;; - do the same with the STR library and/or CL-PPCRE.
;;; - write a top-level instructions that calls our "main" function so that you can call this file as a script from the command line, with sbcl --load AOC-2024-day01.lisp
;;;

Exercise 2 - prepare to parse a grid as a hash-table

This exercise is a short and easy, to prepare you for a harder puzzle. This is not an AOC puzzle itself.

Follow the instructions. We are only warming up.

;; Do this with only CL built-ins,
;; or with the dict notation from Serapeum,
;; or with something else,
;; or all three one after the other.

We will build up a grid stored in a hash-table to represent a map like this:

"....#...##....#"

where the # character represents an obstacle.

In our case the grid is in 1D, it is often rather 2D.

This grid/map is the base of many AOC puzzles.

Take a second: shall we represent a 2D grid as a list of lists, or something else, (it depends on the input size) and how would you do in both cases?

Your turn:

;;
;; 1. Define a function MAKE-GRID that returns an empty grid (hash-table).
;;
(defun make-grid ()
  ;; todo
  )


;;
;; Define a top-level parameter to represent a grid that defaults to an empty grid.
;;

;; def... *grid* ...

;;
;; 2. Create a function named CELL that returns a hash-table with those keys:
;; :char -> holds the character of the grid at this coordinate.
;; :visited or :visited-p or even :visited? -> stores a boolean,
;;  to tell us if this cell was already visited (by a person walking in the map). It defaults
;;  to NIL, we don't use this yet.
;;

(defun cell (char &key visited)
  ;; todo
  )

;;
;; 3. Write a function to tell us if a cell is an obstacle,
;;    denoted by the #\# character
;;
(defun is-block (cell)
  "This cell is a block, an obstacle. Return: boolean."
  ;; todo
  ;; get the :char key,
  ;; check it equals the #\# char.
  ;; Accept a cell as NIL.
  )

We built utility functions we’ll likely re-use on a more complex puzzle.

Let’s continue with parsing the input to represent a grid.

If you are a Lisp beginner or only saw the data structures chapter in my course, I give you the layout of the parse-input function with a loop and you only have to fill-in one blank.

In any case, try yourself. Refer to the Cookbook for loop examples.

;;
;; 4. Fill the grid (with devel data).
;;
;; Iterate on a given string (the puzzle input),
;; create the grid,
;; keep track of the X coordinate,
;; for each character in the input create a cell,
;; associate the coordinate to this cell in the grid.
;;

(defparameter *input* ".....#..#.##...#........##...")

(defun parse-grid (input)
  "Parse a string of input, fill a new grid with a coordinate number -> a cell (hash-table).
  Return: our new grid."
  (loop :for char :across input
        :with grid := (make-grid)
        :for x :from 0
        :for cell := (cell char)
        :do
           ;; associate our grid at the X coordinate
           ;; with our new cell.
           ;; (setf ... )
        :finally (return grid)))

;; try it:
#++
(parse-grid *input*)

That’s only a simple example of the map mechanism that comes regurlarly in AOC.

Here’s the 3rd exercise that uses all of this.

Harder puzzle - hash-tables, grid, coordinates

This exercise comes from Advent Of Code 2024, day 06. https://adventofcode.com/2024/day/6 It’s an opportunity to use hash-tables.

Read the puzzle there! Try with your own input data!

Here are the shortened instructions.

The solutions are in another file, on my GitHub repository.

;;;
;;; ********************************************************************
;;; WARN: this exercise migth be hard if you don't know about functions.
;;; ********************************************************************
;;;
;;; you can come back to it later.
;;; But, you can have a look, explore and get something out of it.

In this exercise, we use:

;;;
;;; parameters
;;; functions
;;; recursivity
;;; &aux in a lambda list
;;; CASE
;;; return-from
;;; &key arguments
;;; complex numbers
;;; hash-tables
;;; the DICT notation (though optional)
;;; LOOPing on a list and on strings
;;; equality for characters

For this puzzle, we make our life easier and we’ use the DICT notation.

(import 'serapeum:dict)

If you know how to create a package, go for it.

Please, quickload the STR library for this puzzle.

#++
(ql:quickload "str")
;; Otherwise, see this as another exercise to rewrite the functions we use.

This is your puzzle input:

;;; a string representing a grid, a map.
(defparameter *input* "....#.....
.........#
..........
..#.......
.......#..
..........
.#..^.....
........#.
#.........
......#...")

;; the # represents an obstacle,
;; the ^ represents a guard that walks to the top of the grid.

When the guard encounters an obstacle, it turns 90 degrees right, and keeps walking.

Our task is to count the number of distinct positions the guard will visit on the grid before eventually leaving the area.

We will have to: - parse the grid into a data structure - preferably, an efficient data structures to hold coordinates. Indeed, AOC real inputs are large. - for each cell, note if it’s an obstacle, if that’s where the guard is, if the cell was already visited, - count the number of visited cells.

;; We'll represent a cell "object" by a hash-table.
;; With Serapeum's dict:
(defun cell (char &key guard visited)
  (dict :char char
        :guard guard
        :visited visited))

;; Our grid is a dict too.
;; We create a top-level variable, mainly for devel purposes.
(defvar *grid* (dict)
  "A hash-table to represent our grid. Associates a coordinate (complex number which represents the X and Y axis in the same number) to a cell (another hash-table).")
;; You could use a DEFPARAMETER, like I did initially. But then, a C-c C-k (recompile current file) will erase its current value, and you might want or not want this.

For each coordinate, we associate a cell.

What is a coordinate? We use a trick we saw in other people’s AOC solution, to use a complex number. Indeed, with its real and imaginary parts, it can represent both the X axis and the Y axis at the same time in the same number.

#|
;; Practice complex numbers:

(complex 1)
;; => 1
(complex 1 1)
;; => represented #C(1 1)

;; Get the imaginary part (let's say, the Y axis):
(imagpart #C(1 1))

;; the real part (X axis):
(realpart #C(1 1))

|#

Look, we are tempted to go full object-oriented and represent a “coordinate” object, a “cell” object and whatnot, but it’s OK we can solve the puzzle with usual data structures.

;; Let's remember where our guard is.
(defvar *guard* nil
  "The guard coordinate. Mainly for devel purposes (IIRC).")

Task 1: parse the grid string.

We must parse the string to a hash-table of coordinates -> cells.

I’ll write the main loop for you. If you feel ready, take a go at it.

(defun parse-grid (input)
  "Parse INPUT (string) to a hash-table of coordinates -> cells."
  ;; We start by iterating on each line.
  (loop :for line :in (str:lines input)
        ;; start another variable that tracks our loop iteration.
        ;; It it incremented by 1 at each loop by default.
        :for y :from 0  ;; up and down on the map, imagpart of our coordinate number.
        ;; The loop syntax with ... = ... creates a variable at the first iteration,
        ;; not at every iteration.
        :with grid = (dict)

        ;; Now iterate on each line's character.
        ;; A string is an array of characters,
        ;; so we use ACROSS to iterate on it. We use IN to iterate on lists.
        ;;
        ;; The Iterate library has the generic :in-sequence clause if that's your thing (with a speed penalty).
        :do (loop :for char :across line
                 :for x :from 0   ;; left to right on the map, realpart of our coordinate.
                 :for key := (complex x y)
                  ;; Create a new cell at each character.
                  :for cell := (cell char)
                  ;; Is this cell the guard at the start position?
                 :when (equal char #\^)
                   :do (progn
                         ;; Here, use SETF on GETHASH
                         ;; to set the :guard keyword of the cell to True.

                         (print "we saw the guard")
                         ;; (setf (gethash ... ...) ...)

                         ;; For devel purposes, we will also keep track of
                         ;; where our guard is with a top-level parameter.
                         (setf *guard* key)
                         )
                  :do
                     ;; Normal case:
                     ;; use SETF on GETHAH
                     ;; to associate this KEY to this CELL in our GRID.
                     (format t "todo: save the cell ~S in the grid" cell)
                  )
        :finally (return grid))
  )

;; devel: test and bind a top-level param for ease of debugging/instropection/poking around.
#++
(setf *grid* (parse-grid *input*))

Task 2: walk our guard, record visited cells.

We have to move our guard on the grid, until it exits it.

I’ll give you a couple utility functions.

(defun is-block (cell)
  "Is this cell an obstacle?"
  ;; accept a NIL, we'll stop the walk in the next iteration.
  (when cell
    (equal TODO #\#)))

;; We choose the write the 4 possible directions as :up :down :right :left.
;; See also:
;; exhaustiveness checking at compile-time:
;; https://dev.to/vindarel/compile-time-exhaustiveness-checking-in-common-lisp-with-serapeum-5c5i

(defun next-x (position direction)
  "From a position (complex number) and a direction, compute the next X."
  (case direction
    (:up (realpart position))
    (:down (realpart position))
    (:right (1+ (realpart position)))
    (:left (1- (realpart position)))))

(defun next-y (position direction)
  "From a position (complex number) and a direction, compute the next Y."
  (case direction
    (:up (1- (imagpart position)))
    (:down (1+ (imagpart position)))
    (:right (imagpart position))
    (:left (imagpart position))))

This is the “big” function that moves the guard, records were it went, makes it rotate if it is against a block, and iterates, until the guard goes out of the map.

Read the puzzle instructions carefuly and write the “TODO” placeholders.

(defun walk (&key (grid *grid*) (input *input*)
               (position *guard*)
               (cell (gethash *guard* *grid*))  ;; todo: *grid* is used here. Fix it so we don't use a top-level variable, but only the grid given as a key argument.
               (direction :up)
               (count 0)
               ;; &aux notation: it saves a nested of LET bindings.
               ;; It's old style.
               ;; Those are not arguments to the function we pass around,
               ;; they are bindings inside the function body.
             &aux next-cell
               next-position
               obstacle-coming)
  "Recursively move the guard and annotate cells of our grid,
  count the number of visited cells."

  ;; At each iteration, we study a new cell we take on our grid.
  ;; If we move the guard to a coordinate that doesn't exist in our grid,
  ;; we stop here.
  (unless cell
    (return-from walk count))

  ;; Look in the same direction first and see what we have.
  (setf next-position
        (complex (next-x position direction) (next-y position direction)))

  (setf next-cell (gethash next-position grid))

  ;; obstacle?
  (setf obstacle-coming (is-block next-cell))

  ;; then change direction.
  (when obstacle-coming
    (setf direction
          (case direction
            (:up :right)
            (:down :left)
            (:right :down)
            (:left :up))))

  ;; Count unique visited cells.
  ;; TODO
  (unless (print "if this CELL is visited...")
      (incf count)
      ;; TODO set this cell as visited.
      (print "set this CELL to visited")
    )

  ;; get our next position now.
  (setf next-position
        (complex (next-x position direction) (next-y position direction)))

  ;; This next cell may or may not be in our grid (NIL).
  (setf next-cell (gethash next-position grid))

  (walk :grid grid :input input
        :cell next-cell
        :position next-position
        :direction direction
        :count count))

and that’s how we solve the puzzle:

(defun part-1 (input)
  (walk :grid (parse-grid input)))

#++
(part-1 *input*)
;; 41
;; The right answer for this input.
;; In AOC, you have a bigger, custom puzzle input. This can lead to surprises.

Closing words

Look at other people’s solutions too. For example, ak-coram’s for our last exercise (using FSet). See how Screamer is used for day 06 by bo-tato (reddit). atgreen (ocicl, cl-tuition, cffi...) solution with a grid as a hash-table with complex numbers. lispm’s day 04 solution. Can you read all solutions?

On other days, I used:

• alexandria’s map-permutations for day 08 when you want... permutations. It doesn’t “cons” (what does that mean you ask? You didn’t follow my course ;) ). Read here: https://dev.to/vindarel/advent-of-code-alexandrias-map-permutations-was-perfect-for-day-08-common-lisp-tip-16il.
• the library fare-memoization, to help in a recursive solution.
• to write math, use cmu-infix. When you spot 2 equations with 2 unknows, think “Cramer system”. This came up last year, so maybe not this year.
• with very large numbers: use double floats, as in 1.24d0
• least common multiple? lcm is a built-in.
• str:match can be a thing to parse strings.
• if you got CIEL (CIEL Is an Extended Lisp), you have Alexandria, cl-str, Serapeum:dict and more libraries baked-in. It’s also an easy way to run Lisp scripts (with these dependencies) from the shell.

See you and happy lisping!

Your best resources:

• the Common Lisp Cookbook
• my course in videos

Table of Contents

1. Building ECL
2. Building WECL
3. Building user programs
4. Extending ASDF
5. Funding

Using Common Lisp in WASM enabled runtimes is a new frontier for the Common Lisp ecosystem. In the previous post Using Common Lisp from inside the Browser I've discussed how to embed Common Lisp scripts directly on the website, discussed the foreign function interface to JavaScript and SLIME port called LIME allowing the user to connect with a local Emacs instance.

This post will serve as a tutorial that describes how to build WECL and how to cross-compile programs to WASM runtime. Without further ado, let's dig in.

Building ECL

To compile ECL targeting WASM we first build the host version and then we use it to cross-compile it for the target architecture.

git clone https://gitlab.com/embeddable-common-lisp/ecl.git
cd ecl
export ECL_SRC=`pwd`
export ECL_HOST=${ECL_SRC}/ecl-host
./configure --prefix=${ECL_HOST} && make -j32 && make install

Currently ECL uses Emscripten SDK that implements required target primitives like libc. In the meantime, I'm also porting ECL to WASI, but it is not ready yet. In any case we need to install and activate emsdk:

git clone https://github.com/emscripten-core/emsdk.git
pushd emsdk
./emsdk install latest
./emsdk activate latest
source ./emsdk_env.sh
popd

Finally it is time to build the target version of ECL. A flag --disable-shared is optional, but keep in mind that cross-compilation of user programs is a new feature and it is still taking shape. Most notably some nuances with compiling systems from .asd files may differ depending on the flag used here.

make distclean # removes build/ directory
export ECL_WASM=${ECL_SRC}/ecl-wasm
export ECL_TO_RUN=${ECL_HOST}/bin/ecl
emconfigure ./configure --host=wasm32-unknown-emscripten --build=x86_64-pc-linux-gnu \
            --with-cross-config=${ECL_SRC}/src/util/wasm32-unknown-emscripten.cross_config \
            --prefix=${ECL_WASM} --disable-shared --with-tcp=no --with-cmp=no

emmake make -j32 && emmake make install

# some files need to be copied manually
cp build/bin/ecl.js build/bin/ecl.wasm ${ECL_WASM}

Running from a browser requires us to host the file. To spin Common Lisp web server on the spot, we can use one of our scripts (that assume that quicklisp is installed to download hunchentoot).

export WEBSERVER=${ECL_SRC}/src/util/webserver.lisp
${ECL_TO_RUN} --load $WEBSERVER
# After the server is loaded run:
# firefox localhost:8888/ecl-wasm/ecl.html

Running from node is more straightforward from the console perspective, but there is one caveat: read operations are not blocking, so if we try to run a default REPL we'll have many nested I/O errors because stdin returns EOF. Running in batch mode works fine though:

node ecl-wasm/ecl.js --eval '(format t "Hello world!~%")' --eval '(quit)'
warning: unsupported syscall: __syscall_prlimit64
Hello world!
program exited (with status: 0), but keepRuntimeAlive() is set (counter=0) due to an async operation, so halting execution but not exiting the runtime or preventing further async execution (you can use emscripten_force_exit, if you want to force a true shutdown)

The produced wasm is not suitable for running in other runtimes, because Emscripten requires additional functions to emulate setjmp. For example:

wasmedge ecl-wasm/ecl.wasm
[2025-11-21 13:34:54.943] [error] instantiation failed: unknown import, Code: 0x62
[2025-11-21 13:34:54.943] [error]     When linking module: "env" , function name: "invoke_iii"
[2025-11-21 13:34:54.943] [error]     At AST node: import description
[2025-11-21 13:34:54.943] [error]     This may be the import of host environment like JavaScript or Golang. Please check that you've registered the necessary host modules from the host programming language.
[2025-11-21 13:34:54.943] [error]     At AST node: import section
[2025-11-21 13:34:54.943] [error]     At AST node: module

Building WECL

The previous step allowed us to run vanilla ECL. Now we are going to use artifacts created during the compilation to create an application that skips boilerplate provided by vanilla Emscripten and includes Common Lisp code for easier development - FFI to JavaScript, windowing abstraction, support for <script type='common-lisp'>, Emacs connectivity and in-browser REPL support.

First we need to clone the WECL repository:

fossil clone https://fossil.turtleware.eu/wecl
cd wecl

Then we need to copy over compilation artifacts and my SLIME fork (pull request) to the Code directory:

pushd Code
cp -r ${ECL_WASM} wasm-ecl
git clone https://github.com/dkochmanski/slime.git
popd

Finally we can build and start the application:

./make.sh build
./make.sh serve

If you want to connect to Emacs, then open the file App/lime.el (it depends on slime and websocket packages), evaluate the buffer and call the function (lime-net-listen "localhost" 8889). Then open a browser at http://localhost:8888/slug.html and click "Connect". A new REPL should pop up in your Emacs instance.

It is time to talk a bit about contents of the wecl repository and how the instance is bootstrapped. These things are still under development, so details may change in the future.

1. Compile wecl.wasm and its loader wecl.js

We've already built the biggest part, that is ECL itself. Now we link libecl.a, libeclgc.a and libeclgmp.a with the file Code/wecl.c that calls cl_boot when the program is started. This is no different from the ordinary embedding procedure of ECL.

The file wecl.c defines additionally supporting functions for JavaScript interoperation that allow us to call JavaScript and keeping track of shared objects. These functions are exported so that they are available in CL env. Moreover it loads a few lisp files:

• Code/packages.lisp: package where JS interop functions reside
• Code/utilities.lisp: early utilities used in the codebase (i.e when-let)
• Code/wecl.lisp: JS-FFI, object registry and a stream to wrap console.log
• Code/jsapi/*.lisp: JS bindings (operators, classes, …)
• Code/script-loader.lisp: loading Common Lisp scripts directly in HTML

After that the function returns. It is the user responsibility to start the program logic in one of scripts loaded by the the script loader. There are a few examples of this:

• main.html: loads a repl and another xterm console (external dependencies)
• easy.html: showcase how to interleave JavaScript and Common Lisp in gadgets
• slug.html: push button that connects to the lime.el instance on localhost

The only requirement for the website to use ECL is to include two scripts in its header. boot.js configures the runtime loader and wecl.js loads wasm file:

<!doctype html>
<html>
  <head>
    <title>Web Embeddable Common Lisp</title>
    <script type="text/javascript" src="boot.js"></script>
    <script type="text/javascript" src="wecl.js"></script>
  </head>
  <body>
    <script type="text/common-lisp">
      (loop for i from 0 below 3
            for p = (|createElement| "document" "p")
            do (setf (|innerText| p) (format nil "Hello world ~a!" i))
               (|appendChild| "document.body" p))
    </script>
  </body>
</html>

I've chosen to use unmodified names of JS operators in bindings to make looking them up easier. One can use an utility lispify-name to have lispy bindings:

(macrolet ((lispify-operator (name)
             `(defalias ,(lispify-name name) ,name))
           (lispify-accessor (name)
             (let ((lisp-name (lispify-name name)))
               `(progn
                  (defalias ,lisp-name ,name)
                  (defalias (setf ,lisp-name) (setf ,name))))))
  (lispify-operator |createElement|)    ;create-element
  (lispify-operator |appendChild|)      ;append-child
  (lispify-operator |removeChild|)      ;remove-child
  (lispify-operator |replaceChildren|)  ;replace-children
  (lispify-operator |addEventListener|) ;add-event-listener
  (lispify-accessor |innerText|)        ;inner-text
  (lispify-accessor |textContent|)      ;text-content
  (lispify-operator |setAttribute|)     ;set-attribute
  (lispify-operator |getAttribute|))    ;get-attribute

Note that scripts may be modified without recompiling WECL. On the other hand files that are loaded at startup (along with swank source code) are embedded in the wasm file. For now they are loaded at startup, but they may be compiled in the future if there is such need.

When using WECL in the browser, functions like compile-file and compile are available and they defer compilation to the bytecodes compiler. The bytecodes compiler in ECL is very fast, but produces unoptimized bytecode because it is a one-pass compiler. When performance matters, it is necessary to use compile on the host to an object file or to a static library and link it against WECL in file make.sh – recompilation of wecl.wasm is necessary.

Building user programs

Recently Marius Gerbershagen improved cross-compilation support for user programs from the host implementation using the same toolchain that builds ECL. Compiling files simple: use target-info.lisp file installed along with the cross-compiled ECL as an argument to with-compilation-unit:

;;; test-file-1.lisp
(in-package "CL-USER")
(defmacro twice (&body body) `(progn ,@body ,@body))

;;; test-file-1.lisp
(in-package "CL-USER")
(defun bam (x) (twice (format t "Hello world ~a~%" (incf x))))

(defvar *target*
  (c:read-target-info "/path/to/ecl-wasm/target-info.lsp"))

(with-compilation-unit (:target *target*)
  (compile-file "test-file-1.lisp" :system-p t :load t)
  (compile-file "test-file-2.lisp" :system-p t)
  (c:build-static-library "test-library"
                          :lisp-files '("test-file-1.o" "test-file-2.o")
                          :init-name "init_test"))

This will produce a file libtest-library.a. To use the library in WECL we should include it in the emcc invocation in make.sh and call the function init_test in Code/wecl.c before script-loader.lisp is loaded:

/* Initialize your libraries here, so they can be used in user scripts. */
extern void init_test(cl_object);
ecl_init_module(NULL, init_test);

Note that we've passed the argument :load to compile-file – it ensures that after the file is compiled, we load it (in our case - its source code) using the target runtime *features* value. During cross-compilation ECL includes also a feature :cross. Loading the first file is necessary to define a macro that is used in the second file. Now if we open REPL in the browser:

> #'lispify-name
#<bytecompiled-function LISPIFY-NAME 0x9f7690>
> #'cl-user::bam
#<compiled-function COMMON-LISP-USER::BAM 0x869d20>
> (cl-user::bam 3)
Hello world 4
Hello world 5

Extending ASDF

The approach for cross-compiling in the previous section is the API provided by ECL. It may be a bit crude for everyday work, especially when we work with a complex dependency tree. In this section we'll write an extension to ASDF that allows us to compile entire system with its dependencies into a static library.

First let's define a package and add configure variables:

(defpackage "ASDF-ECL/CC"
  (:use "CL" "ASDF")
  (:export "CROSS-COMPILE" "CROSS-COMPILE-PLAN" "CLEAR-CC-CACHE"))
(in-package "ASDF-ECL/CC")

(defvar *host-target*
  (c::get-target-info))

#+(or)
(defvar *wasm-target*
  (c:read-target-info "/path/to/ecl-wasm/target-info.lsp"))

(defparameter *cc-target* *host-target*)
(defparameter *cc-cache-dir* #P"/tmp/ecl-cc-cache/")

ASDF operates in two passes – first it computes the operation plan and then it performs it. To help with specifying dependencies ASDF provides five mixins:

• DOWNWARD-OPERATION: before operating on the component, perform an operation on children - i.e loading the system requires loading all its components.

• UPWARD-OPERATION: before operating on the component, perform an operation on parent - i.e invalidating the cache requires invalidating cache of parent.

• SIDEWAY-OPERATION: before operating on the component, perform the operation on all component dependencies - i.e load components that we depend on

• SELFWARD-OPERATION: before operating on the component, perform operations on itself - i.e compile the component before loading it

• NON-PROPAGATING-OPERATION: a standalone operation with no dependencies

Cross-compilation requires us to produce object file from each source file of the target system and its dependencies. We will achieve that by defining two operations: cross-object-op for producing object files from lisp source code and cross-compile-op for producing static libraries from objects:

(defclass cross-object-op (downward-operation) ())

(defmethod downward-operation ((self cross-object-op))
  'cross-object-op)

;;; Ignore all files that are not CL-SOURCE-FILE.
(defmethod perform ((o cross-object-op) (c t)))

(defmethod perform ((o cross-object-op) (c cl-source-file))
  (let ((input-file (component-pathname c))
        (output-file (output-file o c)))
    (multiple-value-bind (output warnings-p failure-p)
        (compile-file input-file :system-p t :output-file output-file)
      (uiop:check-lisp-compile-results output warnings-p failure-p
                                       "~/asdf-action::format-action/"
                                       (list (cons o c))))))

(defclass cross-compile-op (sideway-operation downward-operation)
  ())

(defmethod perform ((self cross-compile-op) (c system))
  (let* ((system-name (primary-system-name c))
         (inputs (input-files self c))
         (output (output-file self c))
         (init-name (format nil "init_lib_~a"
                            (substitute #\_ nil system-name
                                        :test (lambda (x y)
                                                (declare (ignore x))
                                                (not (alpha-char-p y)))))))
    (c:build-static-library output :lisp-files inputs
                                   :init-name init-name)))

(defmethod sideway-operation ((self cross-compile-op))
  'cross-compile-op)

(defmethod downward-operation ((self cross-compile-op))
  'cross-object-op)

We can confirm that the plan is computed correctly by running it on a system with many transient dependencies:

(defun debug-plan (system)
  (format *debug-io* "-- Plan for ~s -----------------~%" system)
  (map nil (lambda (a)
             (format *debug-io* "~24a: ~a~%" (car a) (cdr a)))
       (asdf::plan-actions
        (make-plan 'sequential-plan 'cross-compile-op system))))

(debug-plan "mcclim")

In Common Lisp the compilation of subsequent files often depends on previous definitions. That means that we need to load files. Loading files compiled for another architecture is not an option. Moreover:

• some systems will have different dependencies based on features
• code may behave differently depending on the evaluation environment
• compilation may require either host or target semantics for cross-compilation

There is no general solution except from full target emulation or the client code being fully aware that it is being cross compiled. That said, surprisingly many Common Lisp programs can be cross-compiled without many issues.

In any case we need to be able to load source code while it is being compiled. Depending on the actual code we may want to specify the host or the target features, load the source code directly or first compile it, etc. To allow user choosing the load strategy we define an operation cross-load-op:

(defparameter *cc-load-type* :minimal)
(defvar *cc-last-load* :minimal)

(defclass cross-load-op (non-propagating-operation) ())

(defmethod operation-done-p ((o cross-load-op) (c system))
  (and (component-loaded-p c)
       (eql *cc-last-load* *cc-load-type*)))

;;; :FORCE :ALL is excessive. We should store the compilation strategy flag as a
;;; compilation artifact and compare it with *CC-LOAD-TYPE*.
(defmethod perform ((o cross-load-op) (c system))
  (setf *cc-last-load* *cc-load-type*)
  (ecase *cc-load-type*
    (:emulate
     (error "Do you still believe in Santa Claus?"))
    (:default
     (operate 'load-op c))
    (:minimal
     (ext:install-bytecodes-compiler)
     (operate 'load-op c)
     (ext:install-c-compiler))
    (:ccmp-host
     (with-compilation-unit (:target *host-target*)
       (operate 'load-op c :force :all)))
    (:bcmp-host
     (with-compilation-unit (:target *host-target*)
       (ext:install-bytecodes-compiler)
       (operate 'load-op c :force :all)
       (ext:install-c-compiler)))
    (:bcmp-target
     (with-compilation-unit (:target *cc-target*)
       (ext:install-bytecodes-compiler)
       (operate 'load-op c :force :all)
       (ext:install-c-compiler)))
    (:load-host
     (with-compilation-unit (:target *host-target*)
       (operate 'load-source-op c :force :all)))
    (:load-target
     (with-compilation-unit (:target *cc-target*)
       (operate 'load-source-op c :force :all)))))

To estabilish a cross-compilation dynamic context suitable for ASDF operations we'll define a new macro WITH-ASDF-COMPILATION-UNIT. It modifies the cache directory, injects features that are commonly expected by various systems, and configures the ECL compiler. That macro is used while the

;;; KLUDGE some system definitions test that *FEATURES* contains this or that
;;; variant of :ASDF* and bark otherwise.
;;;
;;; KLUDGE systems may have DEFSYSTEM-DEPENDS-ON that causes LOAD-ASD to try to
;;; load the system -- we need to modify *LOAD-SYSTEM-OPERATION* for that. Not
;;; to be conflated with CROSS-LOAD-UP.
;;; 
;;; KLUDGE We directly bind ASDF::*OUTPUT-TRANSLATIONS* because ASDF advertised
;;; API does not work.
(defmacro with-asdf-compilation-unit (() &body body)
  `(with-compilation-unit (:target *cc-target*)
     (flet ((cc-path ()
              (merge-pathnames "**/*.*"
                               (uiop:ensure-directory-pathname *cc-cache-dir*))))
       (let ((asdf::*output-translations* `(((t ,(cc-path)))))
             (*load-system-operation* 'load-source-op)
             (*features* (remove-duplicates
                          (list* :asdf :asdf2 :asdf3 :asdf3.1 *features*))))
         ,@body))))

Note that loading the system should happen in a different environment than compiling it. Most notably we can't reuse the cache. That's why cross-load-op must not be a dependency of cross-compile-op. Output translations and features affect the planning phase, so we need estabilish the environment over operate and not only perform. We will also define functions for the user to invoke cross-compilation, to show cross-compilation plan and to wipe the cache:

(defun cross-compile (system &rest args
                      &key cache-dir target load-type &allow-other-keys)
  (let ((*cc-cache-dir* (or cache-dir *cc-cache-dir*))
        (*cc-target* (or target *cc-target*))
        (*cc-load-type* (or load-type *cc-load-type*))
        (cc-operation (make-operation 'cross-compile-op)))
    (apply 'operate cc-operation system args)
    (with-asdf-compilation-unit () ;; ensure cache
      (output-file cc-operation system))))

(defun cross-compile-plan (system target)
  (format *debug-io* "-- Plan for ~s -----------------~%" system)
  (let ((*cc-target* target))
    (with-asdf-compilation-unit ()
      (map nil (lambda (a)
                 (format *debug-io* "~24a: ~a~%" (car a) (cdr a)))
           (asdf::plan-actions
            (make-plan 'sequential-plan 'cross-compile-op system))))))

(defun cross-compile-plan (system target)
  (format *debug-io* "-- Plan for ~s -----------------~%" system)
  (let ((*cc-target* target))
    (with-asdf-compilation-unit ()
      (map nil (lambda (a)
                 (format *debug-io* "~24a: ~a~%" (car a) (cdr a)))
           (asdf::plan-actions
            (make-plan 'sequential-plan 'cross-compile-op system))))))

(defun clear-cc-cache (&key (dir *cc-cache-dir*) (force nil))
  (uiop:delete-directory-tree
   dir
   :validate (or force (yes-or-no-p "Do you want to delete recursively ~S?" dir))
   :if-does-not-exist :ignore))

;;; CROSS-LOAD-OP happens inside the default environment, while the plan for
;;; cross-compilation should have already set the target features.

(defmethod operate ((self cross-compile-op) (c system) &rest args)
  (declare (ignore args))
  (unless (operation-done-p 'cross-load-op c)
    (operate 'cross-load-op c))
  (with-asdf-compilation-unit ()
    (call-next-method)))

Last but not least we need to specify input and output files for operations. This will tie into the plan, so that compiled objects will be reused. Computing input files for cross-compile-op is admittedly hairy, because we need to visit all dependency systems and collect their outputs too. Dependencies may take various forms, so we need to normalize them.

(defmethod input-files ((o cross-object-op) (c cl-source-file))
  (list (component-pathname c)))

(defmethod output-files ((o cross-object-op) (c cl-source-file))
  (let ((input-file (component-pathname c)))
    (list (compile-file-pathname input-file :type :object))))

(defmethod input-files ((self cross-compile-op) (c system))
  (let ((visited (make-hash-table :test #'equal))
        (systems nil))
    (labels ((normalize-asdf-system (dep)
               (etypecase dep
                 ((or string symbol)
                  (setf dep (find-system dep)))
                 (system)
                 (cons
                  (ecase (car dep)
                    ;; *features* are bound here to the target.
                    (:feature
                     (destructuring-bind (feature depspec) (cdr dep)
                       (if (member feature *features*)
                           (setf dep (normalize-asdf-system depspec))
                           (setf dep nil))))
                    ;; INV if versions were incompatible, then CROSS-LOAD-OP would bark.
                    (:version
                     (destructuring-bind (depname version) (cdr dep)
                       (declare (ignore version))
                       (setf dep (normalize-asdf-system depname))))
                    ;; Ignore "require", these are used during system loading.
                    (:require))))
               dep)
             (rec (sys)
               (setf sys (normalize-asdf-system sys))
               (when (null sys)
                 (return-from rec))
               (unless (gethash sys visited)
                 (setf (gethash sys visited) t)
                 (push sys systems)
                 (map nil #'rec (component-sideway-dependencies sys)))))
      (rec c)
      (loop for sys in systems
            append (loop for sub in (asdf::sub-components sys :type 'cl-source-file)
                         collect (output-file 'cross-object-op sub))))))

(defmethod output-files ((self cross-compile-op) (c system))
  (let* ((path (component-pathname c))
         (file (make-pathname :name (primary-system-name c) :defaults path)))
    (list (compile-file-pathname file :type :static-library))))

At last we can cross compile ASDF systems. Let's give it a try:

ASDF-ECL/CC> (cross-compile-plan "flexi-streams" *wasm-target*)
-- Plan for "flexi-streams" -----------------
#<cross-object-op >     : #<cl-source-file "trivial-gray-streams" "package">
#<cross-object-op >     : #<cl-source-file "trivial-gray-streams" "streams">
#<cross-compile-op >    : #<system "trivial-gray-streams">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "packages">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "mapping">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "ascii">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "koi8-r">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "mac">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "iso-8859">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "enc-cn-tbl">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "code-pages">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "specials">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "util">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "conditions">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "external-format">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "length">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "encode">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "decode">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "in-memory">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "stream">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "output">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "input">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "io">
#<cross-object-op >     : #<cl-source-file "flexi-streams" "strings">
#<cross-compile-op >    : #<system "flexi-streams">
NIL
ASDF-ECL/CC> (cross-compile "flexi-streams" :target *wasm-target*)
;;; ...
#P"/tmp/ecl-cc-cache/libs/flexi-streams-20241012-git/libflexi-streams.a"

Note that libflexi-streams.a contains all objects from both libraries flexi-streams and trivial-gray-streams. All artifacts are cached, so if you remove an object or modify a file, then only necessary parts will be recompiled.

All that is left is to include libflexi-streams.a in make.sh and put the initialization form in wecl.c:

extern void init_lib_flexi_streams(cl_object);
ecl_init_module(NULL, init_lib_flexi_streams);.

This should suffice for the first iteration for cross-compiling systems. Next steps of improvement would be:

• compiling to static libraries (without dependencies)
• compiling to shared libraries (with and without dependencies)
• compiling to an executable (final wasm file)
• target system emulation (for faithful correspondence between load and compile)

The code from this section may be found in wecl repository

Funding

This project is funded through NGI0 Commons Fund, a fund established by NLnet with financial support from the European Commission's Next Generation Internet program. Learn more at the NLnet project page.

For a long time I’ve used a little macro to time chunks of code to avoid an endless succession of boilerplate functions to do this. I’ve finally published the wretched thing.

If you’re writing programs where you care about performance, you often want to be able to make programatic comparisons of performance. time doesn’t do this, since it just reports things. Instead you want something that runs a bit of code a bunch of times and then returns the average time, with ‘a bunch of times’ being controllable. timing is that macro. Here is a simple example:

(defun dotimes/in-naturals-ratio (&key (iters 10000000) (tries 1000))
  (declare (type fixnum iters)
           (optimize speed))
  (/
   (timing (:n tries)
     (let ((s 0))                       ;avoid optimizing loop away
       (declare (type fixnum s))
       (dotimes (i iters s)
         (incf s))))
   (timing (:n tries)
     (let ((s 0))
       (declare (type fixnum s))
       (for ((_ (in-naturals iters t)))
         (incf s))))))

and then, for instance

> (dotimes/in-naturals-ratio)
1.0073159

All timing does is to wrap up its body into a function and then call a function which calls this function the number of times you specify and averages the time, returning that average as a float.

There are some options which let it print a progress note every given number of calls, wrap a call to time around things so you get, for instance, GC reporting, and subtract away the same number of calls to an empty function to try and account for overhead (in practice this is not very useful).

That’s all it is. It’s available in version 10 of my Lisp tools:

• documentation here;
• git repo here;
• tarball here.

It is with great pleasure and satisfaction that I published new videos about Common Lisp data structures on my course.

The content is divided into 9 videos, for a total of 90 minutes, plus exercises, and comprehensive lisp snippets for each video so you can practice right away.

The total learning material on my course now accounts for 8.40 hours, in 10 chapters and 61 videos, plus extras. You get to learn all the essentials to be an efficient (Common Lisp) developer: CLOS made easy, macros, error and condition handling, iteration, all about functions, working with projects, etc. All the videos have english subtitles.

• learn more about this course (and why it’s a good idea to support me ;) ) on the GitHub page: Common Lisp course in videos: learn Lisp in videos (github),
• and register here: 🎥 Common Lisp programming course on Udemy
  • if you are a student, drop me an email for a free link.
• You can refer to the course with this link (with my referral).

Table of Contents

• What is this course anyways?
• Course outcome
• Chapter content
• Closing words

What is this course anyways?

Hey, first look at what others say about it!

[My employees] said you do a better job of teaching than Peter Seibel.

ebbzry, CEO of VedaInc, August 2025 on Discord. O_o

🔥 :D

I have done some preliminary Common Lisp exploration prior to this course but had a lot of questions regarding practical use and development workflows. This course was amazing for this! I learned a lot of useful techniques for actually writing the code in Emacs, as well as conversational explanations of concepts that had previously confused me in text-heavy resources. Please keep up the good work and continue with this line of topics, it is well worth the price!

@Preston, October of 2024 <3

Now another feedback is that also according to learners, the areas I could improve are: give more practice activities, make the videos more engaging.

I worked on both. With the experience and my efforts, my flow should be more engaging. My videos always have on-screen annotations about what I’m doing or have complementary information. They are edited to be dynamic.

You have 9 freely-available videos in the course so you can judge by yourself (before leaving an angry comment ;) ). Also be aware that the course is not for total beginners in a “lisp” language. We see the basics (evaluation model, syntax...), but quickly. Then we dive in “the Common Lisp way”.

I also created more practice activities. For this chapter on data structures, each video comes with its usual set of extensive lisp snippets to practice (for example, I give you a lisp file with all sequence functions, showing their common use and some gotchas), plus 3 exercises, heavily annotated. Given the time of the year we are on, I prepare you for Advent Of Code :) I drive you into how you can put your knowledge in use to solve its puzzles. If you have access to the course and you are somewhat advanced, look at the new exercise of section 6.

Enough talk, what will you learn?

Course outcome

The goals were:

• give you an overview of the available data structures in Common Lisp (lists and the cons cell, arrays, hash-tables, with a mention of trees an sets)
• teach you how things work, don’t read everything for you. I show you the usual sequence functions, but I don’t spend an hour listing all of them. Instead I give you pointers to a reference and a lisp file with all of them.
• give pointers on where is Common Lisp different and where is Common Lisp similar to any other language. For example, we discuss the time complexity of list operations vs. arrays.
• teach common errors, such as using '(1 2 3) with a quote instead of the list constructor function, and how this can lead to subtle bugs.
• make your life easier: working with bare-bones hash-tables is too awkward for my taste, and was specially annoying as a beginner. I give you workarounds, in pure CL and with third-party libraries.
  • 🆓 this video is free for everybody, hell yes, this was really annoying to me.
• present the ecosystem and discuss style: for example I point you to purely-functional data-structures libraries, we see how to deal with functions being destructive or not destructive and how to organize your functions accordingly.

So, suppose you followed this chapter, the one about functions, and a couple videos on iteration: you are ready to write efficient solutions to Advent Of Code.

Chapter content

3.1 Intro [🆓 FREE FOR ALL]

Common Lisp has more than lists: hash-tables (aka dictionaries), arrays, as well as sets and tree operations. Linked lists are made of “CONS” cells. You should adopt a functional style in your own functions, and avoid the built-ins that mutate data. We see how, and I give you more pointers for modern Common Lisp.

3.2 Lists: create lists, plists, alists

What we see: how to create lists (proper lists, plists and alists). A first warning about the ‘(1 2 3) notation with a quote.

• PRACTICE: list creation

3.3 Lists (2): lists manipulation

Lists, continued. What we see: how to access elements: FIRST, REST, LAST, NTH...

• PRACTICE: accessing sequences elements
• PRACTICE: sequences manipulation functions
• EXERCISE: parse, sort, compute. AOC day 01. (hard for total beginners. Have a look, take at least something out of it)

3.4 Equality - working with strings gotcha

What we see: explanation of the different equality functions and why knowing this is necessary when working with strings. EQ, EQL, EQUAL, EQUALP (and STRING= et all) explained. Which is too low-level, which you’ll use most often.

• PRACTICE: using equality predicates.

3.5 Vectors and arrays

What we see: vectors (one-dimensional arrays), multi-dimensional arrays, VECTOR-PUSH[-EXTEND], the fill-pointer, adjustable arrays, AREF, VECTOR-POP, COERCE, iteration across arrays (LOOP, MAP).

• EXERCISE: compare lists and vectors access time.

3.6 The CONS cell

A “CONS cell” is the building block of Common Lisp’s (linked) lists. What do “cons”, “car” and “cdr” even mean?

3.7 The :test and :keys arguments

All CL built-in functions accept a :TEST and :KEY argument. They are great. What we see: when and how to use them, when working with strings and with compound objects (lists of lists, lists of structs, etc).

3.8 Hash-tables and fixing their two ergonomic flaws [🆓 FREE FOR ALL]

Hash-tables (dictionaries, hash maps etc) are efficient key-value stores. However, as a newcomer, I had them in gripe. They were not easy enough to work with. I show you everything that’s needed to work with hash-tables, and my best solution for better ergonomics.

• PRACTICE: the video snippet to create hash-tables, access and set content, use Alexandria, Serapeum’s dict notation, iterate on keys and values, serialize a HT to a file and read its content back.

3.9 Using QUOTE to create lists is NOT THE SAME as using the LIST function. Gotchas and solution.

Thinking that ‘(1 2 3) is the same as (list 1 2 3) is a rookie mistake and can lead to subtle bugs. Demo, explanations and simple rule to follow.

At last, EXERCISE of section 6: real Advent Of Code puzzle.

;;;
;;; In this exercise, we use:
;;;
;;; top-level variables
;;; functions
;;; recursivity
;;; &aux in a lambda list
;;; CASE
;;; return-from
;;; &key arguments
;;; complex numbers
;;; hash-tables
;;; the DICT notation (optional)
;;; LOOPing on a list and on strings
;;; equality
;;; characters literal notation

(defparameter *input* "....#.....
.........#
..........
..#.......
.......#..
..........
.#..^.....
........#.
#.........
......#...")

Closing words

Thanks for your support, thanks to everybody who took the course or who shared it, and for your encouragements.

If you wonder why I create a paid course and you regret it isn’t totally free (my past me would def wonder), see some details on the previous announce. The short answer is: I also contribute free resources.

Keep lisping and see you around: improving the Cookbook or Lem, on the Fediverse, reddit and Discord...

What should be next: how the Cookbook PDF quality was greatly improved thanks to Typst. Stay tuned.

Oh, a last shameless plug: since Ari asked me at the beginning of the year, I now do 1-1 Lisp coaching sessions. We settled on 40 USD an hour. Drop me an email! (concatenate 'string "vindarel" "@" "mailz" "." "org").

🎥 Common Lisp course in videos

🕊